Kringla, bagel eller bulle? Årets Nobelpris i fysik visar bland annat att vissa märkliga egenskaper hos ett material kan förklaras på samma sätt som antalet hål avgör om brödet är en kringla eller en bulle. Under vissa förhållanden kan till exempel den elektriska ledningsförmågan fördubblas hos ett material.
Bild: iStock
FYSIK: Därför är materien som en kringla
När materiens smådelar länkas ihop kan det under rätt förhållanden uppstå exotiska och oväntade tillstånd. Årets Nobelpris i fysik går till tre forskare som har hjälpt oss att förstå denna märkliga värld. Deras avgörande redskap är den matematik som kan skilja en fralla från en kringla.
Under extrema förhållanden kan material uppföra sig på vardagsfrämmande sätt, till exempel bli supraledande, så att de släpper fram ström helt utan motstånd. Årets Nobelpristagare i fysik – David Thouless, Duncan Haldane och Michael Kosterlitz – har undersökt hur sådana material uppför sig i en platt värld, i tunna filmer som kan betraktas som om de helt saknade tjocklek. Där har de upptäckt en helt ny typ av exotiska materialegenskaper.
Det som belönas är ett helt knippe teoretiska genombrott. Det banbrytande, som förenar de tre pristagarna, är att de har använt sig av en sorts matematik som kallas topologi. Topologin är en gren av matematiken som är släkt med geometrin, men som handskas med egenskaper som består även när former böjs eller töjs. I topologin har en fralla och en giffel samma sorts form, eftersom det går att knåda om den ena till den andra utan att riva eller skära. Däremot hör en bagel till en annan kategori, för det är ett hål i den – och en kringla går ännu ett steg – den har två hål.
Det är inte så svårt att förstå att det antingen finns ett hål i en bulle eller inte. Oavsett hur stor eller liten bullen är så går det inte att skapa ett halvt hål. Men för att hänga med i vad detta betyder för materialen, krävs att tanken får ta ett skutt från bakverken in i en matematisk rymd där formerna finns. Den matematiska kringlan jäser då inte i längd och bredd och höjd, utan till exempel i energi och rörelsemängd, eller andra egenskaper som behövs för att formulera beskrivningen av materialet.
Kringlans hål kan förklara förvandlingen Teoretiska genombrott kan se ut som rena tankelekar, men i årets fysikpris ser vi hur de kan få stor betydelse. En gren av matematiken som kallas topologi visade sig användbar för att beskriva fenomen och fasövergångar i riktigt tunna skikt, så tunna att de kan behandlas som om de har längd och bredd men ingen höjd. Nu är många forskare sysselsatta med så kallade topologiska material, även i tre dimensioner.
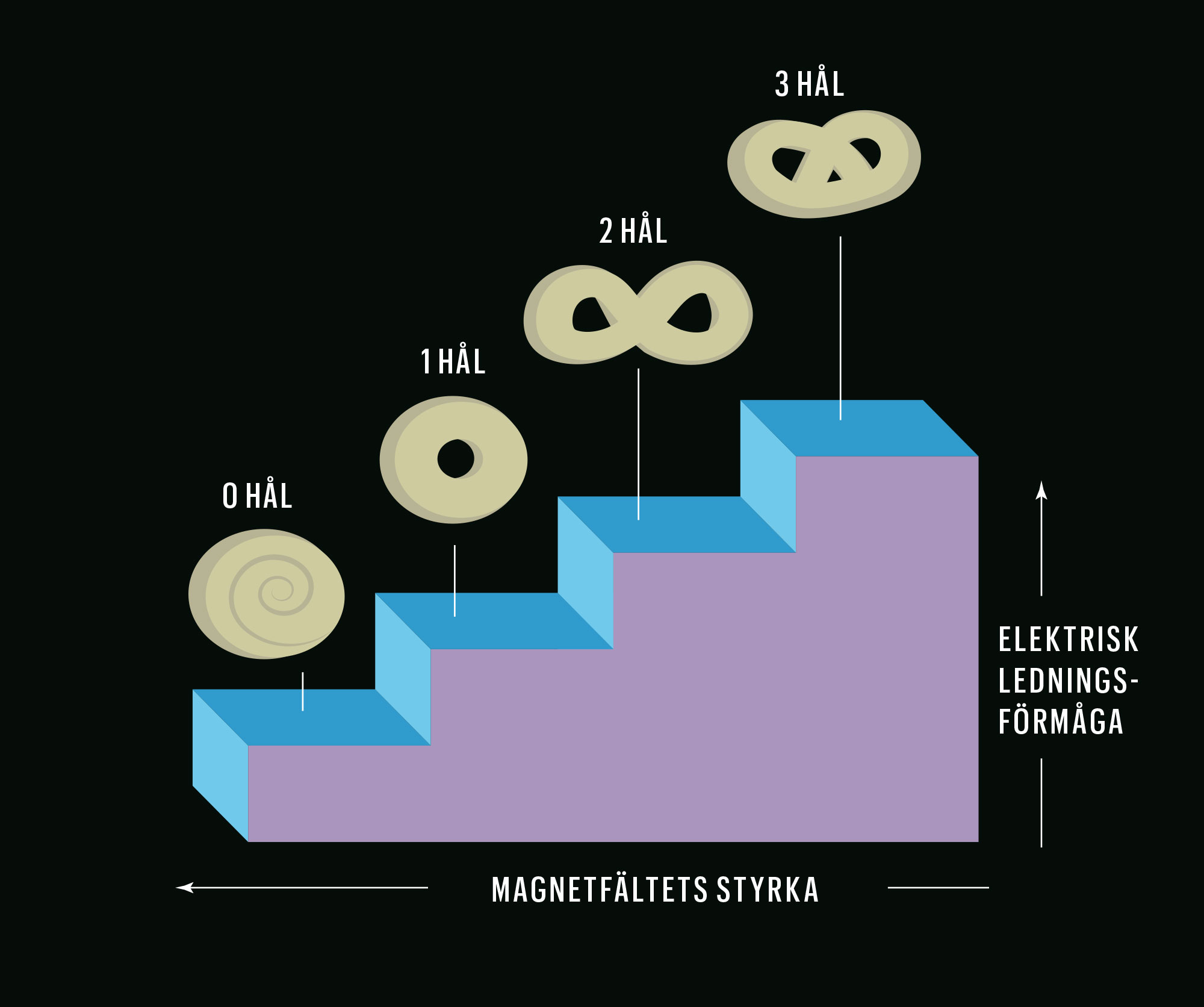
Topologi Bullarna illustrerar den typ av matematik som beskriver egenskaper som ändras i steg. Det går inte att göra ett halvt hål. Så är det till exempel i den kvantiserade Halleffekten – ledningsförmågan i ett material ändras i steg när det befinner sig i ett magnetfält som varieras.
Bild: Johan Jarnestad
Fantastiskt nog motsvarar de här matematiska begreppen fenomen som tydligt går att mäta. Ett exempel är hur den elektriska ledningsförmågan i tunna skikt förändras i distinkta trappsteg när det påverkas av ett magnetfält. Strömmen flyter exakt lika lätt när magnetfältet sakta ändras, ända tills den plötsligt börjar flyta exakt dubbelt så lätt, och så småningom exakt tre gånger så lätt, och så vidare.
Den här kvantiserade Halleffekten, som den kallas, sätter strålkastarljuset på så märkvärdiga ting att den har varit med i Nobelprissammanhang två gånger tidigare: 1985 och 1998.
Det David Thouless gjorde för förståelsen av effekten var att han ställde upp en beskrivning av ledningsförmågan i magnetfältet som knyter den till topologin. En viktig komponent i hans formel uppför sig precis som antalet hål i olika former av småbröd. Den kan alltså bara ändras i heltalssteg.
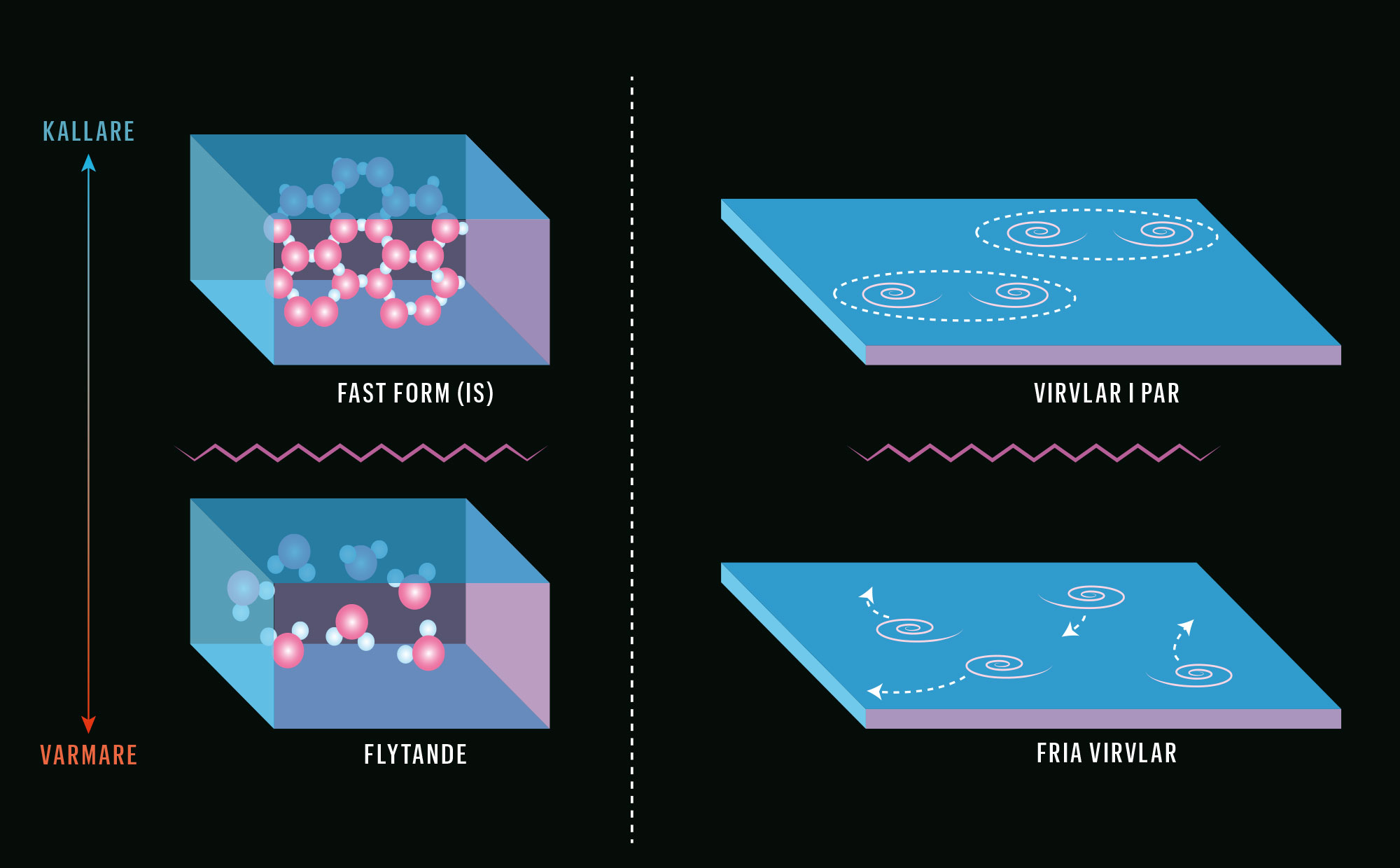
Fasövergång Ett vardagligt exempel på en fasövergång är hur vatten fryser och smälter. Det kan jämföras med mer främmande fasövergångar i platta skikt.
Bild: Johan Jarnestad
Topologin beskriver flera olika typer av sådana trappstegsegenskaper som kallas för topologiska invarianter. Det fina med att den här matematiken har visat sig finnas i material är att det pekar på en sorts stabilitet. En topologisk invariant är inte känslig för störningar. Duncan Haldane beskrev andra sådana topologiskt skyddade egenskaper som uppkommer i endimensionella kedjor eller trådar och ytterligare andra i tunna skikt.
En annan av del av årets Nobelpris handlar om fasövergångar. Det kan jämföras med hur till exempel vatten uppför sig när det fryser eller smälter. Flytande vatten är likadant från alla håll: Molekylerna rör sig om varandra åt alla håll, och ingen riktning skiljer sig från någon annan. I en iskristall sitter vattenmolekylerna i stället fast i raka rader som pekar ut tydliga plan och vinklar. Vattnet har gjort en skarp övergång från en typ av ordning till en annan. Topologiska materiefaser är väldigt annorlunda, men den viktiga insikten är att de också har övergångar där ett tillstånd tvärt går över till ett annat. Där hänger ordningen ihop med topologiska strukturer i stället för med hur molekylerna radar upp sig.
Michael Kosterlitz och David Thouless har beskrivit en fasövergång i tunna skikt där den topologiska ordningen utgörs av en sorts virvlar. Vid extrem kyla kan det finnas virvlar som är bundna i par och alltid följs åt. När temperaturen stiger släpper virvlarna taget om varandra och ger sig av en och en på egen hand. Då ändrar sig materialets egenskaper. Med stadiga virvelpar kan materialet vara supraledande, men när paren löses upp försvinner den egenskapen.
Anledningen till att det här blev så banbrytande är att beskrivningen går att använda i många olika sammanhang. Samma virvelformulering gäller också för till exempel vissa magnetiska material i tunna skikt, eller för en vätska som kan vara supraflytande och rinna utan friktion.
När David Thouless, Duncan Haldane och Michael Kosterlitz började använda topologin för att beskriva material i endimensionella trådar och tvådimensionella tunna skikt lade de grunden till något nytt. Andra forskare har byggt vidare på det och utforskat fler material som kan beskrivas med topologiska verktyg. Topologiska material kallas de, och numera utforskas sådana också i tre dimensioner.
En av dem som arbetar med teorin för topologiska material är Annica Black-Schaffer, fysiker vid Uppsala universitet.
– Mycket av min forskning bygger på Nobelpristagarnas arbeten. Inte så att jag använder deras resultat rakt av, men de har lagt grunden till hela forskningsområdet topologiska material.
Det finns mer märklig fysik i materialen än de flesta av oss känner till. Ibland framställs fysiken som en vetenskap vars mål är att bända isär materian och identifiera de enskilda byggstenarna. Men materialforskare gör ofta tvärtom. De intresserar sig för de fenomen som uppstår när många partiklar samverkar. Tänk på hur fiskar simmar i stim. Fiskstimmet är ett kollektivt fenomen, något som inte går att förstå genom att studera en ensam fisk i en guldfiskskål.
– I ett material har vi oerhört många elektroner. Så vi får ännu mer kollektiva effekter än i ett fiskstim, säger Annica Black-Schaffer.
Topologin i materialen är exempel på sådana kollektiva fenomen, mönster som framträder när delarna i materialet samverkar.
I ett material med skyddade topologiska egenskaper kan små fel eller störningar inte påverka vad som händer. Jämför med trappstegen i den kvantiserade Halleffekten – en knuff som är för svag för att puffa upp systemet till nästa trappsteg kommer inte att påverka egenskaperna över huvud taget. Annica Black-Schaffer arbetar med att söka efter topologiska kvanttillstånd. Hon vill identifiera sådana tillstånd, se hur bra topologiska skydd fungerar, och tänka ut sätt att använda dem för att till exempel lagra information eller göra beräkningar. Det är nämligen just de här robusta egenskaperna som gör att topologiska material ofta nämns som en lovande väg mot att kunna skapa kvantdatorer.
– Kvantsystem är känsliga och kan lätt förstöras. Om kvanttillståndet är topologiskt skyddat finns det hopp att det ska vara mycket mer stabilt.
Om topologin bevarar de annars ömtåliga systemen skulle det kunna gå att skapa fler sådana tillstånd, och att slippa hålla dem extremt nedkylda och isolerade.
Annica Black-Schaffers forskning är bara ett av skotten på den forskningsgren som har växt fram ur de arbeten som belönas med Nobelpriset i fysik i år. Pristagarnas arbete låter sig inte så lätt sammanfattas i några enkla meningar, men det är värt att veta att topologiska material är en stor sak i forskarvärlden. Kringlornas matematik har öppnat en värld av nya fenomen att studera.
David J. Thouless

Född i Storbritannien den 21 september 1934. Professor vid University of Washington i Seattle, USA.
J. Michael Kosterlitz

Född i Storbritannien den 22 juni 1942. Professor vid Brown university, USA.
Duncan M. Haldane

Född i Storbritannien den 14 september 1951. Professor vid Princeton university, USA.

Prenumerera på Forskning & Framsteg!
10 nummer om året och dagliga nyheter på webben med vetenskapligt grundad kunskap.