Ett, tu, tre!

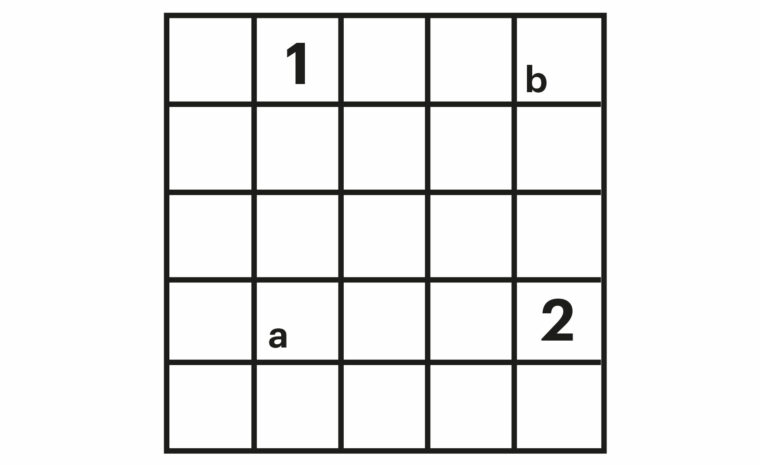
Varje ruta i nätet innehåller ett av talen 1, 2 eller 3. Talen i den sista raden är så placerade att varje nästa siffra (från vänster till höger) inte är mindre än föregående. Två av talen, en 1:a och en 2:a, är redan utplacerade.

Fyll i övriga rutor så att följande villkor uppfylls:

Skärningen av två godtyckliga kolonner och två rader definierar fyra ”hörnrutor” (som i figuren rutorna med 1, 2, a och b). Kravet är att de två summorna av talen i motstående hörn alltid ska vara olika. Till exempel måste a + b vara skilt från 1 + 2 = 3. Det finns bara en lösning till uppgiften.