5 472 730 538 olika sudoku
Allt började med Leonard Euler, en schweizisk matematiker som levde mellan åren 1707 och 1783. Ett år före sin död publicerade han en artikel som handlade om ”en ny sorts magiska kvadrater”. I dag kallar vi dem latinska kvadrater.
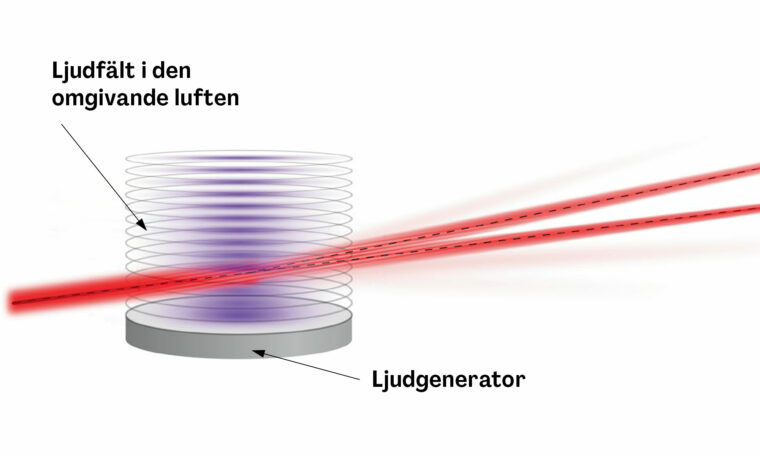
En latinsk kvadrat består av ett rutnät med lika många kolumner som rader. I varje ruta ska det finnas en symbol, oftast ett tal. Antalet olika tal som får användas är detsamma som antalet rader (eller kolumner, de är ju lika många). Rutorna ska dessutom vara ifyllda på ett sådant sätt att varje symbol förekommer en enda gång i varje kolumn och på varje rad.
Miljarder sudoku
En sudoku är en speciell latinsk kvadrat med nio rader och nio kolumner, alltså 81 rutor. De ska fyllas med siffrorna 1 till 9. Det som skiljer sudoku från andra latinska kvadrater är det så kallade boxvillkoret: nätet är indelad i nio mindre kvadrater, så kallade boxar. De omfattar vardera 353 rutor, och kravet är att även de nio rutorna i varje box ska innehålla siffrorna 1-9.Pusslet går ut på att finna slutkonfigurationen utifrån ett begränsat antal rutor som är ifyllda i förväg. Ett välkonstruerat pussel har bara en enda lösning.
Det finns 6 670 903 752 021 072 936 960 olika sudoku. Det svaret kom först alldeles nyligen från den tyske matematikern Bertram Felgenhauer. Men en hel del av dessa sudoku liknar egentligen varandra. I princip är det ingen skillnad om man byter plats på symbolerna på vissa sätt, om till exempel alla 1:or byter plats med alla 2:or. Pusslet förändras inte heller om man ändrar ordningen på de första tre raderna i nätet. Det finns ytterligare flera sådana sätt som man kan flytta om symbolerna och i grunden egentligen ha samma sudoku.
Om man i stället räknar antalet unika pussel blir antalet möjliga sudoku betydligt mindre. Ed Russell och Frazer Jarvis från Storbritannien lyckades nyligen visa att det finns 5 472 730 538 väsentligt olika sudokukonfigurationer. Men med tanke på att var och en av dessa dessutom kan vara slutprodukten av tusentals startkonfigurationer kan vi vara lugna för att antalet olika sudokupussel är tillräckligt många.
Från USA till Japan
Sudokupusslet är faktiskt inte ursprungligen japanskt utan föddes i USA för ett kvartssekel sedan. Det allra första publicerades 1979 i tidskriften Dell Puzzle Magazine under namnet Number Place, men det vann ingen större uppmärksamhet. Senare dök pusslet upp i Japan, som har en gammal tradition för liknande logiska spel.I Japan fick pusslet först namnet Suuji wa dokushin ni kagiru, vilket betyder ”siffra som måste förbli ensam”. Snart förkortade man det till Su Doku, ”ensam siffra”. I Japan införde man också en estetisk förbättring: de från början ifyllda rutorna bildar ett symmetriskt mönster i nätet.
Efter Japan kom pusslet till Storbritannien, också ett land med lång pusseltradition. Därefter exporterades idén till bland annat Sverige.
I de sudoku som finns i dagspressen brukar antalet rutor som är ifyllda från början variera mellan 20 och 35. I de flesta fall är ett pussel med få ifyllda rutor svårare än ett med många ifyllda. Men det går att konstruera riktigt svåra pussel som också har många ifyllda rutor.
En intressant fråga är förstås hur få rutor man behöver ha ifyllda från början för att ändå få en entydig lösning. Rekordet hittills är 17, men det är inte bevisat att det inte skulle kunna vara färre. Det finns fler än 20 000 pussel med bara sjutton ifyllda rutor. Dessa pussel är dock inte symmetriskt ifyllda från början. För symmetriska pussel är det minsta antalet 18 ifyllda rutor.
En annan fråga som saknar svar handlar om det största antalet ifyllda rutor där varje ruta faktiskt behövs för en entydig lösning. Med andra ord, om man tar bort vilken som helst av de ursprungliga siffrorna så kommer pusslet att sakna en entydig lösning. För närvarande är det största antalet 32.
Ytterligare frågor som kan vara värda att närmare titta på är att konstruera sudoku med så många tomma boxar och rader som möjligt. Än så länge är det bästa resultatet ett pussel med fyra helt tomma boxar och ett pussel där antalet helt tomma boxar och rader tillsammans är nio.
Den svåraste sudokun
En sudoku kan göras hur svår som helst, särskilt om man betraktar sudokus med fler kolumner och rader än nio. Sudoku tillhör en klass av problem som i matematiken kallas NP-problem (nondeterministic polynomial time problems). Det innebär att tiden det tar för en dator att finna lösningen växer exponentiellt, det vill säga extremt kraftigt, som en funktion av antalet rader och kolumner hos en sudoku. Att så är fallet bevisades nyligen av Takayuki Yato och Tahashiro Seta vid Tokyos universitet.Mer exakt bevisade de att sudoku är NP-komplett, vilket betyder att soduku tillhör gruppen av de allra svåraste problemen i NP-klassen. Och här snuddar de vid ett av de hetaste områdena inom matematikforskningen, nämligen om NP-problem kan lösas med snabbare algoritmer eller om det inte finns några sådana möjligheter. Svaret på frågan har en prislapp på en miljon dollar donerade av Clay Mathematics Institute i USA.
Ortogonal sudoku
När Euler introducerade de latinska kvadraterna år 1782 gjorde han det genom att formulera ett speciellt problem: sex regementen skickar var sin delegation bestående av sex officerare med sex olika grader till ett möte. Kan dessa 36 officerare ställas i en kvadrat på sådant sätt att ingen rad eller kolumn innehåller två officerare av samma rang och inte heller två officerare från samma regemente?Om problemet förenklas så att man bortser från antingen officerarnas rang eller regemente kan det beskrivas som en enkel latinsk kvadrat med sex rader och sex kolumner. Det finns 812 851 200 olika sådana kvadrater.
Men om man tar hänsyn både till rang och regemente så blir problemet betydligt mer komplext. Man måste då använda två latinska kvadrater där det, om man lägger dem på varandra, inte finns två rutor som innehåller samma grad och regemente. Sådana par av kvadrater kallas för ortogonala latinska kvadrater. I Eulers fall, med sex rader och sex kolumner, finns inga sådana par av kvadrater.
Euler observerade att om hans exempel hade rört 3, 4, 5 eller 7 regementen och lika många officersgrader hade det funnits en lösning, men för just 6 regementen och 6 grader fann han ingen lösning. Det dröjde ända till år 1900 innan fransmannen Gaston Tarry bevisade att Euler hade rätt och att hans uppgift verkligen saknar lösning.
Om vi ökar antalet kolumner och rader till nio finns det däremot många par av ortogonala latinska kvadrater. Frågan är om det också går att lägga till boxvillkoret, så att det blir en ortogonal sudoku. Ingen har tidigare försökt göra ortogonala sudokupussel. Men det visar sig gå alldeles utmärkt.
Sudoku och datorer
Som med de flesta logiska pussel ligger utmaningen i sudoku inte enbart i att finna lösningen utan också i att göra det med enbart logiska resonemang. Men på riktigt svåra sudoku fungerar det inte alltid, och man kan bli tvungen att tillgripa brutalare metoder, som att använda en dator.De flesta sudokulösningsprogram är baserade på en relativt enkel metod som prövar sig fram ruta för ruta. Sådana algoritmer leder till en lösning inom några sekunder.
Ett fåtal program innehåller dock metoder som mer liknar dem som mänskliga lösare använder. På senare tid har det dykt upp elegantare algoritmer baserade på matchning och färgläggning av grafer. Flera sudokuprogrammerare tillämpar även så kallad villkorsprogrammering. Dessa algoritmer gör att datorn oftast kan undvika den enkla prövande metoden, men inte alltid. Det svåraste pusslet som presenteras på dessa sidor är just ett sådant exempel som står emot alla i dag tillämpade algoritmer, utom den brutala metoden, förstås.
Handgjorda sudoku
Här på webben har vi under drygt ett år publicerat Paul Vaderlinds handgjorda sudoku. Det har hunnit bli 65 unika pussel. [Nu kan du ladda ner samtliga problem.](/sites/fof.se/resources/sudoku.pdf) ([Här finns en alternativ länk](http://www.mediafire.com/?ynnzmnjwz4z).)
Läs gärna också artiklen i F&F 8/05 där Paul Vaderlind beskriver matematiken bakom sudoku. Där visar han också både förvånansvärt lätta, extremt svåra och helt annorlunda sudokupussel.