NOBELPRISET I KEMI 2011 – Ytans matematik och kvasikristaller

Under senare år har det visat sig att matematiken bakom mönstren är mycket intrikat. Dessutom har man förstått att många matematiska problem kan relateras till mönster, som undersökning av kristallina och andra material. Detta område av matematiken växer nu snabbt.

Periodiska mönster

Hemmafru hittade över hundra variationer av de knepiga femhörningarna.

Redan de gamla grekerna visste att det bara finns tre regelbundna månghörningar som kan fylla planet – den liksidiga triangeln, kvadraten och den regelbundna hexagonen. De icke-regelbundna konvexa månghörningarna (som buktar utåt) kan som högst ha sex sidor för att fylla planet. En godtycklig fyrhörning kan bilda mosaik, även de icke-konvexa. Men för fem- och sexhörningar gäller mycket stränga restriktioner vad avser deras form. Många matematiker har bearbetat detta problem. Regelbundna femhörningar kan till exempel inte fylla planet. För icke-regelbundna femhörningar som kan täcka en plan yta var fem olika klasser kända år 1918, tre nya upptäcktes 1967 och år 1985 ytterligare sex. I dag känner vi till fjorton typer, men vi vet inte om listan är komplett. Antalet mönster som tillhör dessa fjorton är mycket stort. I USA tog Marjorie Rice fram över hundra sådana mönster. Hon är hemmafru utan formell matematisk bakgrund, och på sin webbplats berättar hon att inspirationen kom från en populärvetenskaplig artikel i sonens exemplar av Scientific American.

För konvexa, utåtbuktande sexhörningar känner vi till bara tre klasser som fyller planet.

Icke-periodiska mönster – finns det pusselbitar som bygger bara sådana?

Länge trodde man att alla mosaikmönster som täcker en yta måste kunna upprepa sig periodiskt. Men det visade sig att det är möjligt att arrangera bitarna så att ett icke-periodiskt mönster bildas.

Till exempel kan ett periodiskt arrangemang av identiska kvadratiska bitar enkelt förvandlas till ett icke-periodiskt. Ett annat sätt är att måla bitarna med olika färger – då är de inte identiska, fast de har samma geometriska form.

Ett oändligt antal pusselbitar kan fylla planet, både periodiskt och icke-periodiskt. En mer intrikat fråga är om man kan hitta en mängd olika bitar som tillsammans uteslutande kan bilda ett icke-periodiskt arrangemang. Under lång tid trodde man att det var omöjligt. Tills den unge amerikanen Robert Berger konstruerade ett sådant mönster, först med drygt 20 000 olika bitar, senare med 104 olika pusselbitar. En annan amerikansk matematiker, Raphael Robinson, lyckades minska antalet nödvändiga bitar till 6.

Oräkneligt antal Penrose-mönster upptäckta under de senaste trettio åren

Britten Roger Penrose, professor i matematisk fysik, letade efter en ännu mindre mängd och fann slutligen år 1974 två pusselbitar som fungerar.

Deras form kan varieras, men de mest kända är nog två romber med sidor av samma längd. När de sätts ihop med vissa passningsregler bildas det så kallade Penrose-mönstret, som inte är periodiskt. Det finns ett oräkneligt antal Penrose-mönster – i stället för de två romberna kan man till exempel välja ”pil” och ”drake”.

I många av Penrose-mönstren påträffas det så kallade gyllene talet τ (den grekiska bokstaven tau), vilket är anmärkningsvärt. Så har förhållandet mellan ytorna på de två romberna, och även mellan drake och pil, just det gyllene värdet.

Dessutom behöver man cirka τ gånger så många drakar som pilar för att bilda ett Penrose-mönster, och detsamma gäller romberna. Om mönstret är oändligt stort, blir det relativa antal som man behöver exakt τ.

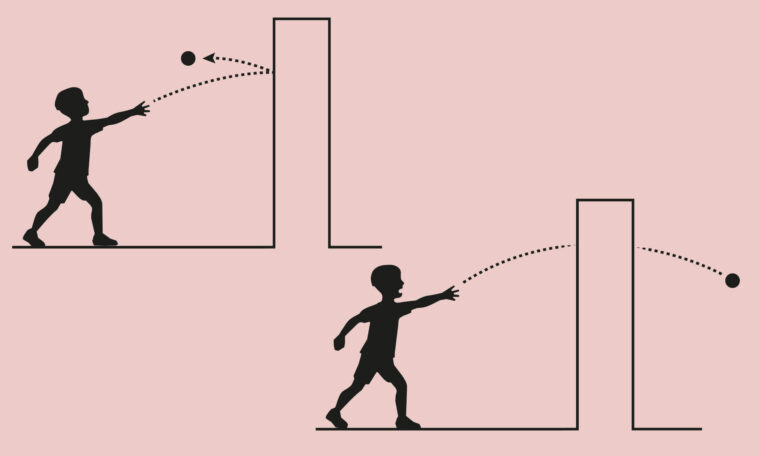
Penrose-mönstren har även andra fascinerande egenskaper. Om man har valt ett visst cirkulärt delmönster med diametern d kan man fråga hur långt man måste gå för att finna ett identiskt delmönster. Det anmärkningsvärda är att avståndet aldrig är större än 2d.

Förhåller sig som ­√2

Finns det då andra par i bitar, som inte baseras på det gyllene talet, och som endast kan bilda icke-periodiska mönster? Ända tills omkring år 1975 var det ett av de mest intrikata problemen i teorin för mönster.

Då hittade den unge matematikern Robert Ammann en serie av icke-periodiska mönster som byggs upp av en kvadrat och en romb. Förhållandet mellan ytorna hos de två bitarna är ­√2 (1,41 ), vilket även gäller förhållandet mellan antalet kvadrater och romber som bildar ett mönster; detta visar också att mönstret är icke-periodiskt.

Det kan anmärkas att förhållandet mellan antalet av de två bitar som behövs för att bilda ett periodiskt mönster, till skillnad från icke-periodiska mönster, är ett rationellt tal (ett tal som kan skrivas som bråk av två heltal). Däremot gäller inte det omvända – mönstret behöver inte vara periodiskt om förhållandet mellan ytorna hos två pusselbitar är ett rationellt tal.

Förbjuden symmetri

Upptäckten av kvasikristaller skakade om mönsterläran.

En perfekt kristall har ett grundmönster som upprepas regelbundet i tre dimensioner. Enligt alla äldre läroböcker i kristallsymmetri kan bara två-, tre-, fyr- eller sextalig symmetri förekomma, medan fem-, sju-, eller högre symmetrier är förbjudna. Det gällde tills kvasikristallerna upptäcktes.

När den israeliske forskaren Dan Shechtman den 8 april 1982 undersökte en metallegering såg han något högst märkligt och oväntat. På bilderna uppvisade hans material en tiotalig symmetri. Varken Shechtman eller hans kolleger hade sett något liknande förut, och det tog två år innan upptäckten kunde publiceras. Den skapade en flodvåg bland fysiker. En febril aktivitet startade nästan omedelbart, och många så kallade ”kvasikristaller” preparerades genom snabbkylning av olika metallegeringar.

Vad var det nu för sorts material? När nyheten om Shechtmans upptäckt blev känd i Sverige skrev Dagens Nyheter den 29 september 1985:

”Ny form på kristallen den fina. Symmetriskt kaos får forskarna att slänga läroböckerna i väggen”.

”Det här innebär att alla läroböcker i elementär kristallografi måste skrivas om”, konstaterade en professor i Stockholm. Men det var en missuppfattning. Läroböckerna är nog så riktiga, men teorierna i dem bygger på att kristaller har en periodisk struktur, vilket kvasikristallen inte har.

De nya materialen, som man kallade kvasikristaller, är icke-periodiska objekt. Medan atomlägen i en klassisk kristall kan beskrivas med hjälp av innehållet i en enda cell, kan en fullständig beskrivning av atomanordningen i en kvasikristall göras bara genom att ange läge för varje atom i hela kvasikristallen.

Samtliga i dag kända kvasikristallina material är metallegeringar. Genom sina speciella egenskaper kan de få stor teknisk betydelse i framtiden. De har dålig värmeledningsförmåga och är mycket hårda. De kan utnyttjas för framställning av mycket hållfasta material.

Upptäckten av kvasikristaller innebär en ny syn på vad som är typiskt för kristallina material. För att beskriva dem använder vi samma matematiska teorier som för periodiska och icke-periodiska mönster.

Islamska arkitekter före sin tid?

Det förefaller som om kvasikristallernas matematik var känd redan på medeltiden.

Länge trodde man att de dekorativa mosaiker som används i den islamska arkitekturen skapades med hjälp av linjal, vinkelhake och passare. Men skulle man ha gjort så, hade vi funnit en massa små fel som dock är sällsynta, hävdar ett par amerikanska forskare. I en nyligen publicerad artikel i tidskriften Science skriver de att islamska mönsterskapare redan under tidig medeltid verkar ha känt till regler för att skapa komplicerade mosaikmönster utifrån fem enkla geometriska figurer. På 1400-talet utvecklades tekniken så att de kunde tillämpa matematiska principer för att konstruera nästan perfekta kvasikristallina mönster.

Stämmer detta var det hela fem sekler innan Roger Penrose och andra västerlänningar efter honom började blottläggga den vackra mosaikens hemligheter.