Tänk dig att du känner på din omgivning med en käpp, utan att titta med ögonen. Så länge du håller käppen i ett fast grepp fungerar den som en förlängning av din arm och du känner de former den stöter emot. Om du däremot håller den ganska löst, då känner du i stället på själva käppen och den fungerar sämre för att känna på andra saker. Poängen är att det inte går att undersöka käppen och att undersöka med käppen samtidigt.

Du måste välja perspektiv.

Det är två olika sätt att uppleva som kompletterar varandra, men som också åtminstone delvis utesluter varandra. De är komplementära.

Exemplet kommer från fysikern Niels Bohr, som använde det för att illustrera en viktig princip i sitt sätt att tänka om såväl fysik som mycket annat.

1947 tog Niels Bohr emot Elefantorden av den danske kungen. När han därmed skulle utforma sin vapensköld prydde han den med den kända kinesiska symbolen för yin och yang – två kontrasterande spiralfält som flyter in i varandra och omsluter varandra. Över symbolen placerade han ett band med frasen ”contraria sunt complementa”: motsatser är komplement.

En av hans viktigaste tankefigurer är just den om komplementaritet. Men han definierade aldrig exakt vad han menade med begreppet. I hans efter­lämnade talmanus och artiklar har vetenskapshistoriker förgäves sökt efter en tydlig definition. Bland Niels Bohrs efterföljare inom fysiken har olika tolkningar förts fram, och somliga anser att komplementariteten förvirrar mer än den förklarar.

– Det var ett luddigt begrepp som han kunde gömma sig bakom, säger Sören Holst, teoretisk fysiker och universitetslektor vid Stockholms universitet.

Niels Bohr fick Nobelpriset i fysik 1922 för sin modell av atomen, och han var en av dem som lade grunden för kvantfysiken. Han var känd för sitt lugna och konverserande sätt. Han ville alltid utveckla sina tankar i samtal. Särskilt berömda är hans diskussioner med Albert Einstein om kvantfysikens natur. Kollegor vittnar om att han var briljant i nära samspråk, men han kunde vara ytterst dunkel i skrift.

Även om det är lite oklart exakt hur Niels Bohr tänkte sig komplementaritet är det tydligt att det finns storheter i fysiken som står emot eller kompletterar varandra på intressanta sätt. De är fascinerande fenomen, även om inte alla är överens om att det är upplysande att samla dem under en gemensam rubrik.

– Det är bättre att tala i mer konkreta termer, till exempel om icke-kompatibla mätningar, säger Sören Holst.

Omkring 1925 började den moderna kvant­mekaniken ta form. Ett mycket hett och omdiskuterat experiment hade gjorts av Otto Stern och Walther Gerlach 1922. De visade att partiklars magnetism – det vi i dag kallar spinn – är kvantiserad på så sätt att den alltid riktar in sig längs den riktning som mätningen görs i. Om mätningen görs horisontellt kommer spinnet att vara riktat åt höger eller vänster, aldrig i någon annan riktning. All information om potentialen för att ha spinn uppåt eller neråt eller på snedden försvinner.

I kvantmekaniken beskrivs en partikel av en vågfunktion, som kan tolkas som en beskrivning av sannolikheten för olika potentiella utfall i en mätning. Efter att mätningen har gjorts försvinner den information som inte är kompatibel med det utfall som konstaterats i mätningen, och den uppmätta egenskapen är den enda som finns kvar.

Det känns konstigt för oss som är vana vid föremål på skalor som är tillgängliga för våra sinnen. I ett experiment med en biljardboll är det i princip möjligt att mäta precis åt vilket håll den snurrar, och det spelar ingen roll i vilken riktning jag placerar min snurrmätare. Det går också att mäta var bollen befinner sig och hur den rör sig, och beskriva hela dess bana.

Så är det inte i kvantmekaniken. En kvantmekanisk biljardboll rör sig på ett suddigt sätt, den existerar som ett moln av sannolikheter. När jag gör en mätning blir det resultatet påtagligt, men de andra delarna av sannolikhetsfunktionen finns inte längre.

– Vad Niels Bohr betonade är att vi aldrig kan tala om egenskaper hos kvantmekaniska objekt om vi inte också talar om hur vi mäter dem, säger Sören Holst.

En aspekt av detta formulerades av fysikern Werner Heisenberg som osäkerhetsrelationen. Den visar att ju noggrannare en partikels läge bestäms, desto mindre går att veta om dess hastighet (eller noga räknat dess rörelsemängd).

Det finns andra par av variabler som fungerar så här, med samma typ av osäkerhetsrelation där den ena blir mer osäker om den andra bestäms noggrannare. Tid och energi är ett sådant par. Ett annat är rörelsemängdsmoment (ett mått på hur mycket ett system snurrar) och riktningen för rotationsaxeln.

Osäkerhetsrelationen kan härledas från en matematisk egenhet i kvantmekaniken. Mätbara egenskaper representeras i kvantmekaniken med något som kallas operatorer i stället för vanliga tal, och det för med sig att de inte kan byta plats med varandra. Med vanliga tal är A×B=B×A, men i kvantmekaniken blir det inte så. Egenskaper som fungerar så att ordningen spelar roll är omöjliga att bestämma samtidigt i ett experiment.

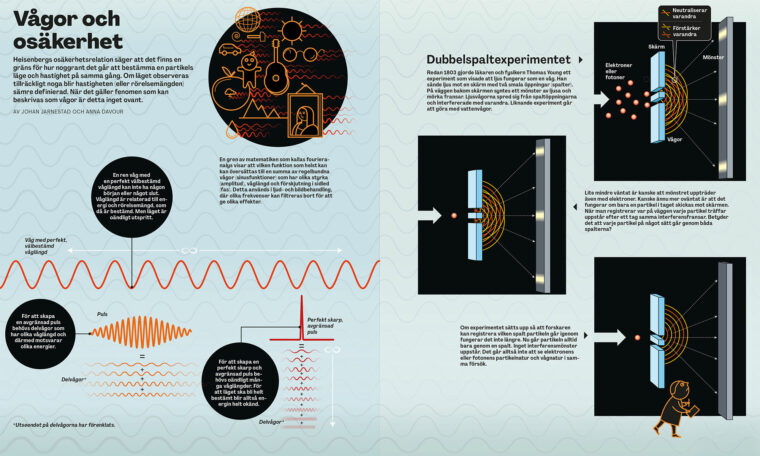
Men osäkerhetsrelationen kan också förstås på ett annat sätt, som kan kännas mer intuitivt för den som är van vid att tänka på vågor.

Fysiker som sysslar med till exempel ljus eller ljud är vana vid att inte kunna definiera läge och energi med samma precision. Rörelsemängden (och energin) i en våg hänger ihop med våglängden. Men för att kunna skapa en avgränsad puls som kan ha ett bestämt läge behövs många delvågor med olika våglängd som kombineras med varandra. Den får då en dåligt definierad rörelsemängd. Omvänt går det att göra en våg med en väl avgränsad våglängd, men den blir då lång och utsmetad i rummet – och det går inte att säga att den har ett bestämt läge.

Osäkerhetsrelationen är alltså inte så märklig, utan väldigt fundamental. Samma sorts osäkerhetsrelation visar sig i fenomen som ljud och ljus, som kan beskrivas med klassisk fysik.

Det som kanske känns märkligt för oss vars sinnen inte är anpassade för kvantvärlden är att vi alls ska prata om partiklar som vågor. Eller att ljus också är partiklar, fotoner. Företeelser i kvantvärlden är både vågor och partiklar, men i varje experiment kommer vi att uppfatta dem som det ena eller det andra. Detta var ett av Niels Bohrs exempel när han talade om komplementaritet.

En situation när det här visar sig kallas för dubbelspaltexperimentet. Där skickas partiklar mot en skärm med två smala springor – spalter – och fångas sedan på andra sidan. Där bildas ett interferensmönster som ser ut som mörka och ljusa fransar, som om partiklarna vore vågor som kommer ut genom de båda spalterna och när de möts förstärker varandra där vågtopparna sammanfaller och släcker ut varandra om en vågtopp möter en vågdal. Det som får folk att haja till är att detta händer även om man bara skickar ut partiklarna en i taget. Går varje partikel genom båda spalterna samtidigt, på något sätt? Det kanske skulle gå att kontrollera, kan man tänka. Men om experimentet ändras för att mäta vilken spalt partiklarna går igenom blir det ingen interferens. Då beter sig partiklarna som små kulor som bara rör sig längs en enkel bana.

Notera att vågor eller partiklar har en annan typ av komplementaritet än i fallet med osäkerhetsrelationen. Här är det fråga om att helt byta perspektiv. Resultaten blir våg eller partikel, interferens eller inte interferens, inte bara att få mer eller mindre osäkerhet i den ena eller andra versionen.

Något som gör det extra svårt att förstå exakt vad Niels Bohr menade med komplementaritet var att hans grundexempel var komplementariteten mellan vad han kallar ”rumtidsbeskrivningen” respektive den ”kausala beskrivningen” av atomen. Vi kan tänka oss att en isolerad atom befinner sig i ett stationärt tillstånd, med elektroner i väldefinierade energinivåer. Det skulle vara rumtidsbeskrivningen. Men det går inte att mäta detta utan att störa tillståndet. För att avläsa tillståndet behövs ett experiment som kan göra det tillgängligt för mänskliga sinnen.

Niels Bohrs funderingar bottnade i hur han som ung fysiker försökte förstå hur atomer fungerar. Det ledde honom till att skapa sin välkända modell där elektronerna rör sig kring atomkärnan, men där de bara har tillgång till vissa fasta banor med olika energi. De flesta av oss har sett olika framställningar av den här modellen, med elektroner som planeter i banor kring en kärna. Atomen kan ta upp eller sända ut energi när elektroner hoppar mellan dessa banor. Elektronernas energi i en given bana kan tolkas som deras rörelseenergi.

Modellen fungerade bra som förklaring av många observationer om atomens struktur. Men något viktigt saknades. I modellen rör sig elektroner i cirkelbanor. Elektroner i böjda banor borde stråla ut energi hela tiden – så gör fria elektroner som inte är i en atom. I så fall skulle elektronerna gradvis tappa energi och röra sig i en spiralbana. Men en av anledningarna till att skapa kvantmekaniken är att energierna i atomen är kvantiserade. Elektroner kan inte förlora energi gradvis, utan bara fånga upp eller göra sig av med energi i paket av bestämd storlek.

Niels Bohr verkar ha brottats med kopplingen mellan rörelseenergi i klassisk fysik och hur den hänger ihop med kvantfysikens energier.

Atommodellen har uppdaterats sedan Niels Bohr ställde upp sin version. Numera visualiseras elektronernas olika nivåer i atomen (”orbitaler”) oftare som sannolikhetsmoln, som visar hur vågfunktionen beskriver dem. Men om ett experiment skulle fånga elektronen, då finns den bara på ett enda ställe och inte utsträckta som vågfunktionen.

På sätt och vis är den komplementaritet Niels Bohr talar om mellan rumtidsbeskrivning och kausal beskrivning densamma som den mellan våg och partikel.

Inom kvantfysiken talade Niels Bohr alltså om flera olika par av företeelser som var komplementära. Han verkar också gärna ha dragit tankespåret vidare och gjort det till ett mer allmänt begrepp, vilket nog har bidragit till att det uppfattas som dunkelt och oprecist. Han talade om komplementaritet inom bland annat biologi. Han funderade också på språket, och om vad som är möjligt att tänka.

I sin bok Det odelbara: Niels Bohr och den moderna fysikens födelse (Fri tanke 2025, första danska utgåvan 1985) argumenterar författaren Tor Nørretranders för att hela Niels Bohrs tänkande kommer ur språkfilosofin. Vi måste ta till klassiska begrepp för att tala om kvantfysiken, eftersom vi måste utgå från det vi uppfattar med våra sinnen – direkt eller indirekt. Det enda språk som finns att tillgå för att tala om fysiken är det som knyter an till vardagsbegreppen, men de räcker inte riktigt till för kvantfysiken. ”Just därför att våra vardagliga bilder varken kan tillämpas eller lämnas därhän måste vi finna oss i komplementariteten”, skriver Tor Nørretranders.

Det finns onekligen ett glapp mellan vardagsvärlden och kvantmekaniken som blir uppenbart i liknelsen med käppen i början av den här artikeln. Du kan enkelt göra en dubbel undersökning av en käpp. Först känner du med käppen, sedan känner du på käppen, och får på så sätt all information om situationen. Det fungerar inte i kvantvärlden. Där gäller det att välja, och sedan finns den komplementära informationen inte kvar. Käppen är en bra metafor, men käppar i människostorlek är inte kvantmekaniska.

I kvantmekaniken går det bara att undersöka en individuell partikel på ett sätt. Efter att en mätning har gjorts är all information om vad den skulle ha uppvisat i den alternativa undersökningen borta. Då är det enda sättet att göra en sådan dubbel undersökning att förbereda många identiska experiment med många likadana partiklar och göra dem alla likadant. Vissa mätningar ger ett utslag, andra ger ett annat, och då går det att lägga ihop resultaten till en statistisk bild av till exempel på vilken sida av ett hinder partiklar befinner sig, eller åt vilket håll deras spinn är riktat. Skillnaden är att du kan undersöka samma käpp på två sätt, men den kvantmekaniska undersökningen går bara att göra en gång på varje partikel.

Fysiker har olika åsikter om begreppet komplementaritet, men Sören Holst tycker inte att det bidrar med något nyttigt.

– Bohr lade den här mattan av oklarhet över hela diskussionen, säger Sören Holst.

Sören Holst påpekar att osäkerhetsrelationen i sig egentligen inte är så konstig – men att den blir märklig i kombination med den speciella roll som mätningar och mätutfall spelar inom kvantmekaniken. Vad är en mätning egentligen, och varför intar den en sådan särställning i teorins formulering?

En tung kritik mot Niels Bohrs tankesätt kom från fysikern John Stewart Bell. Han är känd för Bells olikhet, den teoretiska grunden bakom Nobelpriset i fysik 2022. Han funderade mycket över mätningens roll i kvantmekaniken. Kanske finns det något här som fysiken inte har utforskat tillräckligt.

– Bell påtalade att om kvantmekaniken verkligen utgör en grundläggande teori, som de flesta fysiker antar, så ska vi inte behöva använda begreppet ”mätning” när vi formulerar dess grundpremisser. I stället förväntar vi oss att kvantmekaniken ska tala om för oss vad en mätning är, säger Sören Holst.

Om mycket av det som verkar mystiskt i kvantmekaniken tycks uppstå i samband med att en mätning görs, då kanske det vore viktigt att få ett bättre grepp om just mätningen. Den tolkning av kvantmekaniken som fördes fram i kretsen kring Niels Bohr har fört med sig att den typen av frågor sopats under Bohrs oklarhetsmatta. Sören Holst vill inte slå sig till ro med det.

– Från en fundamental teori ska vi kunna härleda makroskopiska saker, inklusive oss själva. Det projektet kanske misslyckas, men det måste vara ett mål. Och då kan vi inte stoppa in mätningar redan från början, säger Sören Holst.

På det viset ser mätproblemet ut att vara en ingång till att tänka på nya sätt om kvantfysikens grunder. Det kan vara en öppning för att formulera kvantmekaniken på ett nytt sätt. Kanske framstår då komplementariteten i ett nytt ljus.