Smakprov ur ”Tio ekvationer som styr världen”

Vi tänker ofta på matematiken som en hård, objektiv vetenskap. Och det är den: Många av de frågor jag tittar på i Tio ekvationer som styr världen handlar om spel, finansvärlden och algoritmerna i sociala medier. Men matematik kan också hantera mjukare och vardagligare problem, som att bedöma om det är dags att bli rädd när flygplanet skakar extra mycket, eller att avgöra hur generös det är rimligt att vara i kontakten med nya bekanta. Eller för den delen hur länge vi ska titta på en Netflixserie innan vi ger upp, hur vi ska lära av våra erfarenheter, och hur mycket tilltro vi ska ha till våra relationer och karriärval.

Det jag har funnit efter att ha arbetat 25 år med tillämpad matematik är att vare sig frågan är hård eller mjuk är ekvationer något för dig! I boken berättar jag om vad ekvationerna kan säga oss. En av dessa är Bayes ekvation. Den ser invecklad ut, men även utan att sätta dig in i alla detaljer kan du bilda dig en uppfattning om hur den fungerar.

Tänk dig att du är en erfaren flygresenär som har flugit hundra gånger tidigare. Men flygfärden du nu befinner dig mitt uppe i är helt annorlunda. När planet sänker sig inför landning skramlar och skakar det på ett sätt som du aldrig tidigare har varit med om. Det märks på alla dina medpassagerare att de är rädda. Kan det vara sant? Kan det vara så att det allra värsta tänkbara är på väg att hända?

Det du behöver göra är att tänka på den totala andelen flygplan som kraschar – något i stil med 1 på 10 miljoner. Tänk nu på det faktum att detta ”bara” är din värsta flygresa någonsin – det ger 1 av 100 tidigare flygresor. Det betyder att du, teoretiskt sett, om du flög 10 miljoner gånger skulle förvänta dig 100 000 (det vill säga 10 miljoner delat med 100) flygresor som är lika illa eller värre än den du befinner dig på nu. Och bara en av dessa 100 000 flygresor skulle sluta i en krasch. Så … sannolikheten att du är på den förfärliga kraschturen, även om det är skakigt, är 1/100 000 eller 0,001%. Verkligen mycket liten.

Den matematiska ekvation vi använder här kallas Bayes regel. I min bok kallar jag den bedömningsekvationen, därför att det är vad den gör: Den hjälper oss att förbättra våra bedömningar. Låt oss göra om problemet ovan med hjälp av den. Ekvationen är:

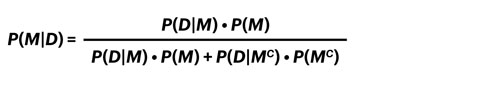
Här står P(M|D) för sannolikheten att modellen gäller givet de data som finns. (P är sannolikhet, M är modell, D är data). I fallet med det skakande planet är modellen M den krasch du föreställer dig i ditt huvud, och datan D är skakningarna du upplever. Du vill veta sannolikheten att planet kommer att krascha givet att det skakar, det vill säga P(M|D).

För att lösa detta behöver du fylla i högersidan av ekvationen. Du vet grundsannolikheten för krascher, 1 på 10 miljoner, P(M)=1/10 000 000. Du vet att flyg som kraschar skakar mycket, så P(D|M)=1. Du vet också av erfarenhet att sannolikheten att flyget inte kommer att krascha (betecknat M^C) är omkring 1 på 100. Med alla dessa tal insatta i Bayes ekvation får vi:

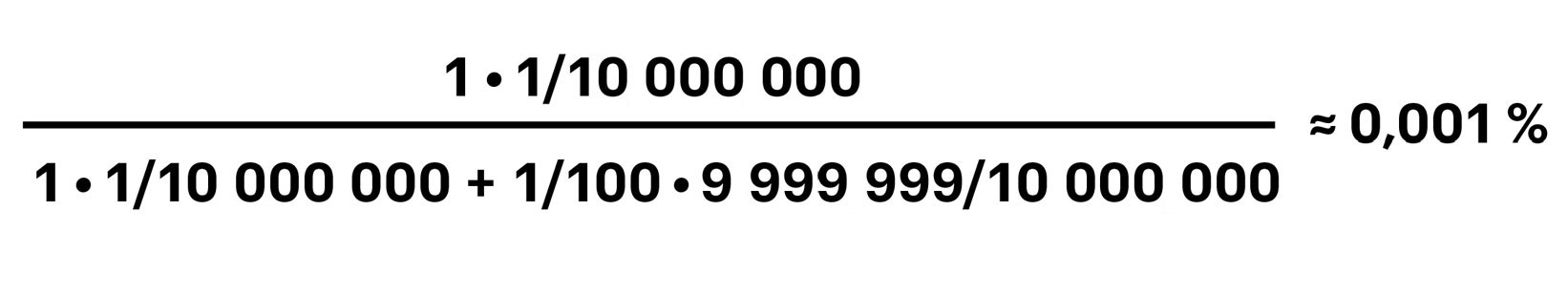
Precis som angivet ovan, en risk på en på hundratusen. Det var inte så svårt va?

Ekvationer är kraftfulla för att de låter oss handskas med alla sorters problem, från att skapa algoritmer för ett sociala medier-företag till våra vardagskontakter med vänner och kollegor. För att se det ska vi ta en titt på ett annat exempel.

Amy är en mycket tillitsfull person och hennes bild av andra är att de är snälla mot henne. Men Amy är gammal nog att veta att alla inte är snälla och hon har också en bitch-model inom sig. Men döm inte Amy efter vilka ord hon sätter på de olika kategorierna människor, det här är ju ändå tankar som hon behåller för sig själv. Så när hon presenteras för Rachel, tjejen som sitter i bänken intill henne när de börjar en ny kurs, utgår hon från att risken att Rachel är en bitch är ganska liten, säg ungefär en på tjugo, dvs. P(M)=1/20.

Den där första morgonen går det trögt för Amy att förstå allt i detalj eftersom man på hennes tidigare skola inte läst in bakgrunden till de begrepp som föreläsaren använder sig av. Och sedan, strax efter lunch, händer något riktigt otrevligt. Amy sitter i all avskildhet i ett av båsen inne på toaletten och surfar på sin mobil. Då hör hon Rachel och en annan tjej komma in.

”Den nya tjejen är dum i huvudet”, säger Rachel. ”Jag försökte förklara kulturell appropriering och hon hade ingen aning om vad uttrycket betyder. Hon trodde att det var som när vita människor försöker lära sig spela bongotrummor!”

Amy sitter blick stilla och tyst och väntar på att de ska gå därifrån. Hur ska hon reagera på detta? Borde Amy trots allt förlåta Rachel för de nedsättande orden och ge henne en chans till?

Det matematiska svaret, enligt Bayes sats, är ett rungande ”Ja”.

För att se varför ska vi sätta den i verket. Innan Amy mötte Rachel hade hon P(M)=1/20. Men vad är P(D | M), sannolikheten för att Rachel dissar Amy på toaletten om hon verkligen är en bitch? Här är det svårt att ange några siffror, men låt oss anta att det är rena lotteriet: P(D | M) = 0,5. Bitchiga människor ägnar minst 50 procent av sin tid åt att prata om andra saker. Om Rachel inte är en bitch så är hon snäll, P(M^C) = 1 – P(M) = 0,95. Vi måste också räkna med sannolikheten för att även snälla människor gör misstag. Låt oss sätta P(D|M^C) = 0,1 som får stå för sannolikheten att en snäll person kan ha en dålig dag av tio och råka säga något som hen senare får anledning att ångra.

Det enda vi nu behöver göra är att utföra beräkningen. Det gör vi på samma sätt som med exemplet på flygplanskraschen, fast med andra siffror:

Sannolikheten för att Rachel är en bitch kan uppskattas till ungefär 1 av 5. Det är skälet till att Amy bör förlåta Rachel. Utsikterna för att hon egentligen är en snäll person är så stora som 4 av 5. Det skulle vara väldigt orättvist att döma henne enbart efter denna enda händelse. Amy gör bäst i att inte ta upp det hon har hört Rachel säga, eller låta de bitchiga orden påverka hur hon uppträder mot henne. Hon gör klokast i att bara vänta och se hur det blir i fortsättningen. Sannolikheten för att de båda mot slutet av terminen kommer att kunna skratta åt det som hände inne på toaletten är så stor som 80 procent.

En ekvation i artiklen har uppdaterats. 

Läs en intervju med David Sumpter här.