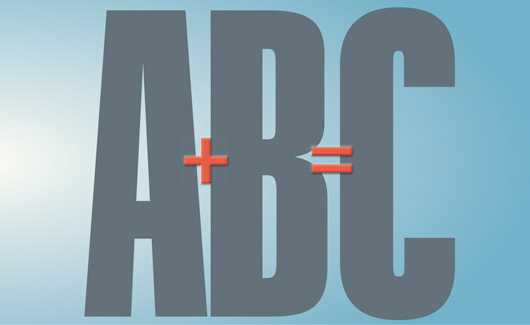
Ett matematiskt genombrott som ingen kan bevisa
Det japanska matematikgeniet Shinichi Mochizuki påstår sig ha löst en av matematikens största gåtor. Men lösningen är så svår att ingen annan matematiker begriper den. Därför kan genombrottet än så länge varken bekräftas eller förkastas.
Den 30 augusti 2012 lade matematikprofessorn i Kyoto, Shinichi Mochizuki, upp en fjärde artikel på sin hemsida. Därmed blev hans livsprojekt fullbordat – i fyra artiklar på sammanlagt 512 sidor presenterar han en helt ny matematisk teori som löser ett centralt problem i talteorin, den så kallade abc-förmodan. Håller teorin för granskning kan den innebära en revolution inom matematiken. Därför har den inter-universella Teichmüller-teorin, som författaren kallar den, blivit hett omdiskuterad bland världens matematiker. Än så länge är det ingen som begriper den. Mochizukis arbete beskrivs som kommet från framtiden eller från yttre rymden – som om en utomjording hade landat på vår planet med ett meddelande på ett främmande språk.
– Jag kan inte ens säga något preliminärt om teorin, för jag begriper den inte, säger Minhyong Kim, professor vid Oxford university i Storbritannien och Pohang university i Sydkorea.
Om någon, så borde just Minhyong Kim kunna uttala sig närmare om teorin. Han har känt Mochizuki sedan ett par decennier, och arbetar inom samma område i matematiken, så kallad anabelsk geometri. Det är en rätt nyutvecklad gren av den aritmetiska geometrin, och det är bara några få i världen som i dag begriper sig på den. Mochizuki är en av de främsta inom området, och i början på 1990-talet, då han bara var drygt 20 år gammal, bidrog han med avgörande arbeten. Sedan dess har han utvecklat sitt teoribygge, de senaste 15 åren nästan helt utan kontakt med omvärlden.
– Jag hoppas han får rätt, säger Minhyong Kim. Men det är för tidigt att säga vilka följder som den nya teorin kan få för hela matematiken. Å andra sidan handlar det om helt grundläggande matematik, sådant som barn behärskar redan på mellanstadiet, som plus och gånger. Går det att säga något helt nytt om detta så blir det omvälvande för hela vårt fält.
Abc-förmodan formulerades relativt nyligen, i mitten av 1980-talet, av två matematiker – britten David Masser och fransmannen Joseph Oesterlé. Till sin grund har den världens enklaste ekvation för heltal, som att räkna ut vad 2 + 3 blir. Med symboler kan den skrivas: a + b = c, och därifrån kommer namnet: abc-förmodan.
Men det är lite mer komplicerat än så. För det handlar om primtal – tal som är delbara bara med 1 och sig själva: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47 och så vidare.
Förmodan hävdar, grovt sett, att de tre talen – a, b och c – inte samtidigt kan innehålla för många identiska primtalsdelare.
– Det är ändå märkligt att vi fortfarande vet så lite om heltalen, säger Ulf Persson, matematikprofessor vid Chalmers tekniska högskola i Göteborg.
– Vi kan dela upp två tal i var sina primtalsfaktorer, och multiplicerar vi de två talen med varandra är det lätt att få fram primtalsfaktorer av resultatet. Men om vi i stället lägger ihop de två talen, så vet vi väldigt lite om primtalsfaktorer av summan. Resultatet verkar mer eller mindre slumpartat. Om abc-förmodan kan bevisas skulle det betyda att vi har lite koll på det hela.
Att hitta ett mönster, ett samband, vilket som helst, som styr primtalen, har varit många matematikers dröm ända sedan de gamla grekerna. Så även om abc-förmodan kan verka esoterisk, har den långtgående konsekvenser för matematiken.
I all sin enkelhet leder den till att många andra matematiska problem inom talteorin kan lösas. Till exempel kan många av de hittills ouppklarade så kallade diofantiska ekvationerna få sin lösning. Namnet diofantiska härstammar från den grekiske matematikern Diofantos från Alexandria, som var verksam under mitten av 200-talet, och studerade heltaliga lösningar till ekvationer.
– I matematiken kan vi fortfarande läsa många gamla skrifter med behållning, ett bibliotek är alltjämt viktigt för oss, säger Ulf Persson. Medan vetenskapliga artiklar inom många andra forskningsfält snabbt blir överflödiga.
Talteorin är inte bara en fråga om abstrakt matematik, påpekar Dorian Goldfeld, professor vid Columbia university i New York. Den har också funnit sina tillämpningar i datavärlden, där sekretessen i våra mejl och internettransaktioner bygger på talteorin och det faktum att alla positiva heltal kan skrivas som produkter av primtal. En populär krypteringsmetod bygger på att hitta stora primtalsfaktorer av ännu större heltal, något som kräver långa räknetider på kraftfulla datorer.
Till de mest berömda diofantiska ekvationerna hör Fermats stora sats från 1637, som handlar om ekvationen an + bn = cn. För n = 2 får man a2 + b2 = c2, alltså den välbekanta Pythagoras sats om sambandet mellan sidorna i en rätvinklig triangel. Men för n större än 2 finns inte några positiva heltalslösningar.
Det är den stora satsen som fransmannen Pierre de Fermat gjorde en anteckning om i marginalen på sitt exemplar av just sin kopia av Diofantos bok Arithmetica. Där påstod han sig ha löst problemet, men inte haft plats i marginalen för att skriva ner sin lösning.
Trots höga prissummor till den som lyckades, tog det ytterligare 350 år, och ett flertal nya matematiska grenar som utvecklades under den tiden, innan Andrew Wiles från Storbritannien knäckte beviset för den stora satsen i september 1994. Då hade han mer eller mindre i hemlighet hängivit sig åt Fermats sats i åtta år.
Han sägs ha bestämt sig för att lösa den redan som tioåring, då han på väg hem från skolan i det lokala biblioteket i Cambridge råkade hitta en bok om Fermat och hans sats och blev förbluffad över att till och med han kunde förstå innebörden.
Fermat själv bevisade sin sats för n = 4. Hundra år senare, i mitten av 1700-talet, visade den schweiziska universalforskaren Leonard Euler att det inte finns någon lösning för n = 3. I början av 1800-talet kom en lösning för n = 5.
– Under hela 1800-talet försökte många bevisa den stora satsen. Det blev drivkraften bakom utvecklingen av nya metoder inom talteorin, säger Juliusz Brzezinski, professor i matematik vid Göteborgs universitet. Och mot slutet av seklet var satsen bevisad för alla n mindre än 100, med bara fyra undantag för 37, 59, 67 och 74. Medan det allmänna beviset höll sig fortsatt ouppnåeligt.
Fermats stora sats handlar om en typisk diofantisk ekvation, menar Dorian Goldfeld i New York. Den är solklar, enkel att formulera och helt galet svår att lösa.
Det största hindret med diofantiska ekvationer har hittills varit att varje problem måste besvaras för sig, från fall till fall. Det har inte funnits någon teori som binder dem samman. Därför har abc-förmodan fått en så viktig roll. Den inbegriper en mängd andra ekvationer i talteorin, både de redan lösta satserna och förmodanden som fortfarande väntar på att lösas. Blir abc-förmodan löst följer de andra med.

Kunskap baserad på vetenskap
Prenumerera på Forskning & Framsteg!
Inlogg på fof.se • Tidning • Arkiv med tidigare nummer
– Jämfört med Fermats stora sats, som egentligen inte är så central för oss, ligger abc-förmodan i hjärtat på talteorin, säger Ulf Persson. Till exempel, tänk att något orakel skulle kommit till oss med en lösning på Fermats stora sats – det hade varit väldigt spännande, men inte påverkat matematiken något nämnvärt.
Abc-förmodan däremot kan lösa många centrala problem som talteorin kämpat med sedan länge, inklusive Fermats sats. Den kommer ut som en direkt konsekvens av abc-förmodan. Är abc-förmodan löst, ryms lösningen av Fermats stora sats på bara en halv sida.
– På det sättet påminner den om ett annat mycket berömt och ännu inte löst problem inom talteorin, den så kallade Riemannhypotesen från 1859. Den har också att göra med primtal, och handlar om hur de fördelas bland alla heltal. Å ena sidan verkar primtalen komma helt slumpmässigt. Å den andra – uppenbarligen helt deterministiskt. Ingen vet. Det finns till och med ett pris på en miljon dollar till den som kommer på lösningen av Riemannhypotesen. Fast om man vill tjäna en miljon dollar, så är nog det här ett av de det svåraste sätten att göra det på, även för mycket framstående matematiker, säger Ulf Persson.
Abc-förmodan må inte vara lika känd som Fermats stora sats, men den anses kunna framkalla en dominoeffekt som ingen ännu förmår överblicka. Om beviset nu stämmer.
Svårigheten är att ta sig igenom Shinichi Mochizukis bevis. Än så länge är han ensam om sin teori. För att lösa detta till synes enkla problem har han byggt upp nya matematiska världar.
– Han har skapat ett helt nytt språk, ett helt nytt universum befolkat av matematiska objekt som vi inte känner igen. Det har han gjort bara för att kunna säga något om de tal och geometriska figurer som vi redan känner till, säger Minhyong Kim.
Frågan är nu hur det ska gå till att granska Mochizukis arbete. Den vedertagna processen med kollegial granskning, den så kallade peer review, är satt ur spel när bara en person i världen talar det språk som teorin är skriven på. Andra stora matematiska upptäckter som har väckt stor uppmärksamhet under den senaste tiden – Andrew Wiles bevis för Fermats stora sats 1994, och Grigorij Perelmans lösning på Poincarés förmodan 2002 – var också extremt komplicerade och krävde en stor arbetsinsats från andra matematiker. Men artiklarna kunde ändå nagelfaras av några som kände igen sig i landskapet. Så är det inte nu.
Mochizukis omfattande teori befinner sig helt utanför det matematiska världsalltet. Att ge sig in i den världen kräver en investering av stor möda och mycket tid, kanske flera år, samtidigt som risken finns att satsningen inte betalas tillbaka, att hela bygget är bristfälligt.
De första 1000 primtalen större än 1:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069 1087 1098 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409 1423 1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499 1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613 1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861 1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933 1949 1951 1973 1979 1987 1993 1997 1999 2003 2011 2017 2027 2029 2039 2053 2063 2069 2081 2083 2087 2089 2099 2111 2113 2129 2131 2137 2141 2143 2153 2161 2179 2203 2207 2213 2221 2237 2239 2243 2251 2267 2269 2273 2281 2287 2293 2297 2309 2311 2333 2339 2341 2347 2351 2357 2371 2377 2381 2383 2389 2393 2399 2411 2417 2423 2437 2441 2447 2459 2467 2473 2477 2503 2521 2531 2539 2543 2549 2551 2557 2579 2591 2593 2609 2617 2621 2633 2647 2657 2659 2663 2671 2677 2683 2687 2689 2693 2699 2707 2711 2713 2719 2729 2731 2741 2749 2753 2767 2777 2789 2791 2797 2801 2803 2819 2833 2837 2843 2851 2857 2861 2879 2887 2897 2903 2909 2917 2927 2939 2953 2957 2963 2969 2971 2999 3001 3011 3019 3023 3037 3041 3049 3061 3067 3079 3083 3089 3109 3119 3121 3137 3163 3167 3169 3181 3187 3191 3203 3209 3217 3221 3229 3251 3253 3257 3259 3271 3299 3301 3307 3313 3319 3323 3329 3331 3343 3347 3359 3361 3371 3373 3389 3391 3407 3413 3433 3449 3457 3461 3463 3467 3469 3491 3499 3511 3517 3527 3529 3533 3539 3541 3547 3557 3559 3571 3581 3583 3593 3607 3613 3617 3623 3631 3637 3643 3659 3671 3673 3677 3691 3697 3701 3709 3719 3727 3733 3739 3761 3767 3769 3779 3793 3797 3803 3821 3823 3833 3847 3851 3853 3863 3877 3881 3889 3907 3911 3917 3919 3923 3929 3931 3943 3947 3967 3989 4001 4003 4007 4013 4019 4021 4027 4049 4051 4057 4073 4079 4091 4093 4099 4111 4127 4129 4133 4139 4153 4157 4159 4177 4201 4211 4217 4219 4229 4231 4241 4243 4253 4259 4261 4271 4273 4283 4289 4297 4327 4337 4339 4349 4357 4363 4373 4391 4397 4409 4421 4423 4441 4447 4451 4457 4463 4481 4483 4493 4507 4513 4517 4519 4523 4547 4549 4561 4567 4583 4591 4597 4603 4621 4637 4639 4643 4649 4651 4657 4663 4673 4679 4691 4703 4721 4723 4729 4733 4751 4759 4783 4787 4789 4793 4799 4801 4813 4817 4831 4861 4871 4877 4889 4903 4909 4919 4931 4933 4937 4943 4951 4957 4967 4969 4973 4987 4993 4999 5003 5009 5011 5021 5023 5039 5051 5059 5077 5081 5087 5099 5101 5107 5113 5119 5147 5153 5167 5171 5179 5189 5197 5209 5227 5231 5233 5237 5261 5273 5279 5281 5297 5303 5309 5323 5333 5347 5351 5381 5387 5393 5399 5407 5413 5417 5419 5431 5437 5441 5443 5449 5471 5477 5479 5483 5501 5503 5507 5519 5521 5527 5531 5557 5563 5569 5573 5581 5591 5623 5639 5641 5647 5651 5653 5657 5659 5669 5683 5689 5693 5701 5711 5717 5737 5741 5743 5749 5779 5783 5791 5801 5807 5813 5821 5827 5839 5843 5849 5851 5857 5861 5867 5869 5879 5881 5897 5903 5923 5927 5939 5953 5981 5987 6007 6011 6029 6037 6043 6047 6053 6067 6073 6079 6089 6091 6101 6113 6121 6131 6133 6143 6151 6163 6173 6197 6199 6203 6211 6217 6221 6229 6247 6257 6263 6269 6271 6277 6287 6299 6301 6311 6317 6323 6329 6337 6343 6353 6359 6361 6367 6373 6379 6389 6397 6421 6427 6449 6451 6469 6473 6481 6491 6521 6529 6547 6551 6553 6563 6569 6571 6577 6581 6599 6607 6619 6637 6653 6659 6661 6673 6679 6689 6691 6701 6703 6709 6719 6733 6737 6761 6763 6779 6781 6791 6793 6803 6823 6827 6829 6833 6841 6857 6863 6869 6871 6883 6899 6907 6911 6917 6947 6949 6959 6961 6967 6971 6977 6983 6991 6997 7001 7013 7019 7027 7039 7043 7057 7069 7079 7103 7109 7121 7127 7129 7151 7159 7177 7187 7193 7207 7211 7213 7219 7229 7237 7243 7247 7253 7283 7297 7307 7309 7321 7331 7333 7349 7351 7369 7393 7411 7417 7433 7451 7457 7459 7477 7481 7487 7489 7499 7507 7517 7523 7529 7537 7541 7547 7549 7559 7561 7573 7577 7583 7589 7591 7603 7607 7621 7639 7643 7649 7669 7673 7681 7687 7691 7699 7703 7717 7723 7727 7741 7753 7757 7759 7789 7793 7817 7823 7829 7841 7853 7867 7873 7877 7879 7883 7901 7907 7919
Å andra sidan – om det skulle visa sig att teorin är invändningsfri, så har det varit värt allt besvär. För då öppnas portar till nya okända världar att utforska.
Ett misstag har faktiskt redan uppdagats. Den unge forskarstudenten Vesselin Dimitrov vid Yale university påpekade för Mochizuki ett fel i hans tredje och fjärde artikel, något som Mochizuki blixtsnabbt besvarade. Det är ett mindre misstag som ska rättas till i en ny version som kommer i januari, skrev han på sin webbsida.
Klarar inte andra att ta sig igenom den okända terrängen kommer bevisbördan att ligga på Mochizuki. Han har redan författat en kortare presentation av teorin och ska i slutet av mars i år presentera sina tankegångar på en konferens i Kyoto. En sällsynt händelse för Mochizuki som väldigt sällan deltar i forskarmöten. Det har gått tolv år sedan han var med på en konferens utanför Japan, och han har avböjt intervjuer sedan artiklarna kom ut i augusti förra året.
– Han reser inte mycket, säger Minhyong Kim, som hör till de närmaste vännerna. Men han är inte heller särskilt asocial. Han ogillar publicitet, bara.
Minhyong Kim träffade Shin, som Mochizuki kallas, 1985. Det var då Mochizuki anlände till Princeton university, 16 år gammal. Sex år senare hade han redan disputerat, och flyttat till Kyoto university där han blev professor – bara 33 år gammal. Mycket ung och mycket begåvad. Är han ett geni?
– Shin är oerhört duktig, säger Minhyong Kim. Men han är också den hårdast arbetande person jag någonsin har träffat. Han ger inte upp förrän han har förstått problemet till fullo. Men ett geni, nej, det är ett alltför simpelt begrepp för att fånga all den mångfald och komplexitet som krävs för att vara kreativ i matematiken.
Mochizuki har uppenbart satsat all sin kreativa kraft på matematiken, och presenterar inte sig själv som en matematiker, utan som en inter-universell geometer.
– Grunden till Mochizukis arbete kommer från en annan berömd matematiker, Alexander Grothendieck i Frankrike, säger Ulf Persson. Under 1960-talet revolutionerade Grothendieck matematiken genom att påbörja en grandios syntes av geometri och talteori. Hans abstrakta begreppsapparat och ett helt nytt matematiskt språk var dock svåra att tillägna sig för en äldre generation matematiker.
Grothendieck är fortfarande en matematisk legend, ännu mer sedan han omkring 1970, vid 40 års ålder, hoppade av från alla sina offentliga uppdrag. Det sägs att han som pacifist och miljövän var upprörd över världens tillstånd. Han avböjde även att ta emot det svenska Crafoordpriset 1988, och drog sig så småningom tillbaka till en hemlig ort i Pyrenéerna.
– Mochizuki introducerades i det grothendieckska landskapet av sin lärare, tysken Gerd Faltings, säger Ulf Persson. Faltings står bakom en annan matematisk milstolpe, ett bevis på den så kallade Mordells förmodan, där lösningar till diofantiska ekvationer knyts till geometriska objekt i Grothendiecks anda. Mochizuki visade sig vara en baddare på att tekniskt tillägna sig det omfattande maskineriet, vilket gör att folk tar honom på fullaste allvar.
När Mochizuki gav sig in i turerna kring abc-förmodan på 1990-talet var den knappt tio år gammal, så han fick hitta egna stigar in i denna talhärva.
– Det intressanta i matematiken är inte själva resultatet, säger Ulf Persson. Det intressanta är vägen fram till beviset, hur man kom på det. Många gånger har det hänt att bevisen varit ihåliga, felaktiga. Ändå kan de leda till nya tankebanor, medan det med andra blir tvärstopp.
Att Mochizukis närmast obegripliga livsverk tas på allvar och inte bara ignoreras av det matematiska etablissemanget beror alltså på att han anses exceptionellt begåvad. Sedan unga år har han gjort sig känd som en självständig och uppfinningsrik forskare som kommit med flera häpnadsväckande resultat. Beroende på hur man räknar, har han slitit med sin teori i två decennier nu, och hela teorin omfattar cirka tusen sidor. Ingen har i princip haft insyn i detta arbete under de senaste 15 åren.
– Det finns så klart en fara i att isolera sig så fullständigt i sin egen värld. Det är lätt hänt att man tappar kontakten med verkligheten och inte kan inse varför andra har svårt att förstå. Men vad som för många matematiker är lockande med Mochizukis teori är dess inre skönhet och elegans. Om den nu håller för granskning.