
En möjlig väg I Nobelpristagarens David Winelands jonfälla representerar olika energi hos varje jon en kvantbit, som manipuleras med laserljus. Det anses vara en lovande metod för att bygga en kvantdator.
Bild: Andrew Brookes, Nationel Physical Laboratory / SPL
Har vi redan skapat kvantdatorn?
Vissa menar att kvantdatorn redan är verklighet, och syftar på en gåtfull låda som kallas D-wave. Men uppfyller den verkligen kraven? Frågan diskuteras livligt i forskarvärlden. Vad är egentligen en riktig kvantdator? Här hjälper Uppsalaforskarna Marie Ericsson och Erik Sjöqvist till att reda ut begreppen.
Det här är en artikel från 2015.
Med buller och bång presenterades den kanadensiska D-wavemaskinen på en presskonferens för nio år sedan. Den marknadsfördes som världens första kommersiella kvantdator och såldes snart till både Google och den amerikanska rymdstyrelsen Nasa. Prislappen låg på flera miljoner amerikanska dollar. Ändå har ingen ännu lyckats visa att det som utspelar sig inne i den svarta boxen verkligen är vad som krävs för att D-wavemaskinen ska kunna anses vara en kvantdator.
D-wavedatorn har visat att den klarar av att lösa vissa optimeringsproblem, som att arrangera en komplicerad bordsplacering eller lösa sudoku. Men det gör den ändå inte till den universella kvantdator som vida skulle överskrida dagens konventionella datorkraft.
Kvantdatorer är ett hett forskningsområde, men samtidigt en knivig utmaning. De lovar fantastisk kapacitet men är mycket ömtåliga och påverkas lätt av omgivningen och förlorar då sin ofantliga beräkningskraft.
En dator är en maskin som behandlar information. Informationen är kodad som olika tillstånd, till exempel olika styrka på elström i en transistor. Det kan låta enkelt, men har vittgående konsekvenser. Det betyder nämligen att hur en dator representerar och behandlar information beror på de spelregler som naturen erbjuder.
Vi vet i dag att dessa spelregler inte tvunget ser ut som de som gäller till vardags, och som kan beskrivas med klassisk fysik. I mikrokosmos, den värld som befolkas av mycket små objekt, som molekyler, atomer och elektroner, ersätts den klassiska fysiken av kvantmekanikens helt annorlunda lagar.
Kvantmekaniken har funnits i nästan nittio år, men idéer om att den kan erbjuda nya möjligheter att konstruera beräkningsmaskiner växte fram under 1970-talet. Nobelpristagaren och fysikern Richard Feynman brukar tillskrivas äran av att ha gett startsignalen i en föreläsning 1982, där han beskrev principerna för en kvantdator.
Våra klassiska datorer är ”antingen/eller”. En liten kiselkrets kodar information i så kallade bitar. En bit anger de logiska värdena för sant eller falskt, vilket är 0 eller 1 i binär matematik, där alla tal representeras av nollor och ettor. I en kvantvärld ersätts den klassiska datorns antingen/eller-bitar av kvantbitar som kan vara både/och. Medan dagens datorer manipulerar bitar, manipulerar kvantdatorn kvantbitar.
En kvantdator består av tre fundamentala byggstenar: kvantbitar, kvantgrindar och resultatmätningar. Informationen kodas först som kvantbitar, vilka blir grunden för beräkningen utförd av kvantgrindarna, och till sist görs en mätning av resultatet – informationen tolkas.
I en kvantbit representeras de logiska värdena 0 eller 1 av ett kvantmekaniskt objekt som kan anta två tillstånd. Till exempel kan två energinivåer i en atom fungera som en kvantbit, eller två polarisationstillstånd hos ljuspartikeln fotonen, eller två olika rotationsriktningar hos en elektron. Till skillnad från en klassisk bit av information, är det möjligt att försätta en kvantbit i ett både/och-tillstånd som beskriver så kallade superpositioner, eller överlagringar av 0 och 1.
Superposition för till exempel en atom som befinner sig i två olika energinivåer, 0 och 1, innebär att atomen med viss sannolikhet befinner sig i var och en av de två energinivåerna 0 och 1. Det är den kvantmekaniska superpositionen som gör att många fler tal kan lagras i kvantdatorer än i konventionella datorer.
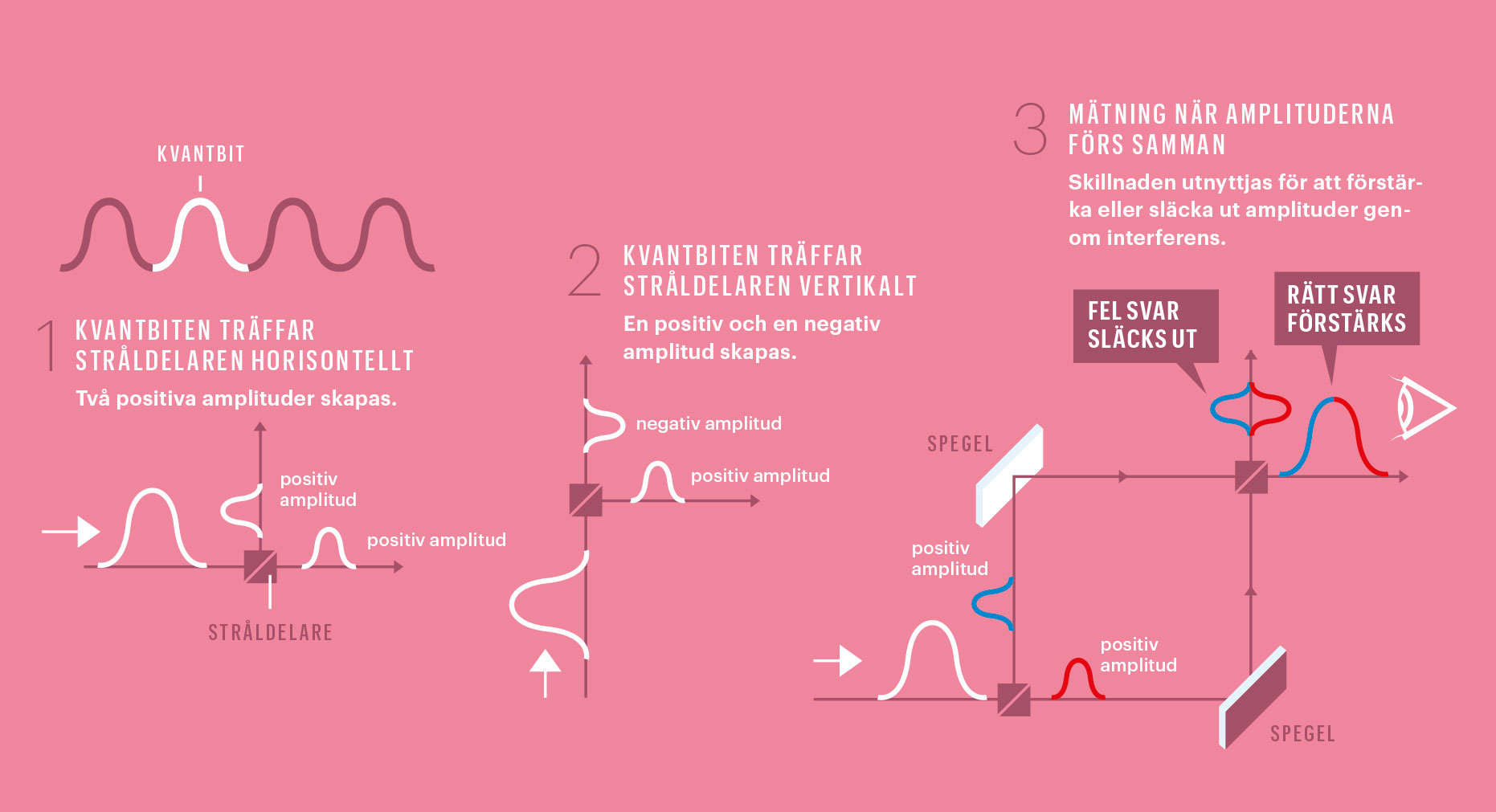
Beräkna med kvantbitar
En vanlig dator räknar med hjälp av bitar som är 1 eller 0. En bit kan till exempel vara elektrisk spänning som är på eller av. En kvantdator använder kvantbitar, som har betydligt fler värden mellan 0 och 1. Det finns flera sätt att skapa en kvantbit, till exempel med en elektron eller en jon i olika energilägen. Enligt kvantfysiken representeras kvantbitar av vågamplituder. När resultatet av beräkningen med flera kvantbitar ska läsas ut utnyttjas därför våginterferens: de felaktiga beräkningarna släcks ut och den rätta dyker fram.
Bild: Johan Jarnestad
I varje stund kan en kvantbit, som till exempel representerar två olika energilägen hos en atom, samtidigt ha värdet 0 och 1. Två sådana kvantbitar kan representera fyra värden: 00, 01, 10 och 11 – motsvarande 0, 1, 2 och 3 i decimala talsystemet. Antalet tal som kan lagras växer exponentiellt med antalet kvantbitar. Om man har tre bitar i en vanlig dator kan bara ett tal mellan 0 och 16 lagras. Med tre kvantbitar kan 23 (2 x 2 x 2 = 8) olika tal lagras i en superposition. Med 1 000 kvantbitar blir antalet tal som kan lagras parallellt 21000, vilket motsvarar ungefär 10300 tal (en etta följd av 300 nollor). Det är fler än det finns partiklar i hela universum.
Hur konstigt det än låter, så är superposition ett vanligt tillstånd hos invånarna i den mikrovärld som kvantmekaniken beskriver. Men det går lätt förlorat när mikrovärlden möter sin omvärld. Vibrationer, elektromagnetism, värme och mycket annat i omgivningen förstör superpositionen och tvingar systemet att välja en av de två överlagrade möjligheterna. Kvanttillståndet försvinner till förmån för ett klassiskt tillstånd och en kvantdator förlorar sin kraft. Det gäller alltså att upprätthålla superpositionen längre än den mikrosekund som det tar för datorn att göra en beräkning. Då blir kvantdatorn oövervinnelig.
För detta räcker det inte med att kunna lagra enorma mängder information, det gäller också att kunna göra beräkningar med kvantbitarna, vilket görs av kvantgrindar. Utmaningen är både att bygga själva kvantgrindarna, hårdvaran, och att skriva mjukvaran, att programmera kvantdatorn. Vanliga program som används i klassiska datorer är oanvändbara i en kvantdator. Det beror på att en kvantdator inte kan utnyttja mellanresultaten för att föra beräkningar vidare. Varje mellanresultat, alltså avläsning av den delikata superpositionen, förstör superpositionstillståndet och beräkningskraften går förlorad.
Genombrottet kom 1994, då matematikern Peter Shor vid Bell labs i USA skapade en algoritm för beräkningar med en kvantdator. För första gången visade han hur det praktiskt kan gå till för att effektivt lösa vissa problem som vanliga datorer inte förmår lösa. Med Shors algoritm skulle en kvantdator kunna ändra spelreglerna för vad som är möjligt att göra. Den kan nämligen lösa en av nyckelfrågorna i vårt digitala samhälle: hur banksekretessen och andra kommersiella och militära hemligheter bäst kan skyddas.
Det vanliga sättet som används för att garantera sekretessen i dag är så kallad faktorisering av primtal. För att faktorisera talet 15 ska man hitta de primtal – tal som är jämnt delbara bara med sig själva och 1 – som multiplicerade med varandra ger talet 15. Rätt svar är 3 och 5, vilket går ganska snabbt att komma på. Det blir betydligt svårare att faktorisera stora tal, som till exempel 47 854 517. Svårigheten att lösa problemet blir i praktiken oöverstiglig om talet växer. Däremot är det lätt att kontrollera om någon påstår att svaret är primtalen 7 919 och 6 043 – det är bara att multiplicera de två talen med varandra.
Denna asymmetri mellan svårigheten att hitta primtalen och lättheten att kontrollera att de är rätt, utnyttjas för att göra säkra banktransaktioner i dag. Sekretessen bygger på att det i praktiken är omöjligt att faktorisera riktigt stora tal. Ett tal bestående av 400 siffror skulle kräva miljarder år av beräkningar med en största superdator i dag. Men en kvantdator, om den gick att konstruera, skulle kunna lösa problemet effektivt.
Nyckelordet här är effektivt. Det betyder att de beräkningsresurser som krävs för att hitta primtalsfaktorerna inte växer för snabbt när storleken på talet som ska faktoriseras växer. Ett mått på effektiviteten hos en kvantberäkning är hur antalet kvantgrindar ökar då storleken på indata ökar. Det är kvantgrindens uppgift att utföra beräkningar av de värden som lagrats i kvantbitarna. För att bygga en generell kvantdator har man visat att det räcker med att grindar verkar på endast en eller två kvantbitar åt gången. Så kan grindarna kombineras till en kvantkrets som ska utföra beräkningar på ett antal kvantbitar enligt ett mönster bestämt av vilken typ av problem som ska lösas.
När det gäller primtalsfaktorisering bestäms effektiviteten av hur mycket antalet kvantgrindar måste ökas då det tal vars primtalsfaktorer vi söker ökar i storlek. För att faktorisera talet 15 behövs uppåt 17 kvantgrindar. Antalet ökar dock inte lika dramatiskt när mycket större tal ska faktoriseras jämfört med en vanlig dator, som inte klarar av att hitta primtalsfaktorer på ett effektivt sätt.
För en kvantdator som programmerats med Shors algoritm skulle det gå på ett ögonblick. Däri ligger kvantdatorns magiska kraft – den räknar inte snabbare, men den verkar inte behöva växa så mycket för stora tal.
Kvantdatorns effektivitet gäller inte bara primtalsfaktorisering. Hittills känner vi till några problem där kvantdatorer är effektivare än vanliga datorer, till exempel utveckling av nya material eller läkemedelsforskning.
Det tredje och sista steget i beräkningar med en kvantdator är mätningen av resultatet. Vi måste få ut bara ett värde när vi vill läsa ut information ur en superposition av många värden. Man kan se superpositionen som en blandning av vågor på vattnet. Vågorna beskriver sannolikheter för att hitta ett visst värde. Det är som att kasta tio små stenar i vattnet och se på vågorna som rör sig och blandas med varandra. Vågorna förstärker och släcker ut varandra och bildar ett så kallat interferensmönster på vattenytan.
Kvantdatorn utnyttjar interferensen för att förstärka sannolikheten för att plocka ut det rätta svaret och släcka ut alla de felaktiga. Det gäller att kombinera kvantgrindar på ett smart sätt för att öka sannolikheten för att rätt svar läses ut vid mätningen.
I teorin går det alltså mycket bra att utföra beräkningar mer effektivt med en kvantdator än med en klassisk dator. Men eftersom verkligheten aldrig är perfekt var det till en början en öppen fråga om huruvida det är möjligt att i praktiken bygga en godtyckligt stor kvantdator. Det beror på att inte ens i de mest robusta kvantbitarna går det att undvika felen. De är än mer besvärliga i en kvantdator än i en vanlig dator, eftersom antalet fel växer exponentiellt med antalet kvantbitar.
Ett sätt att korrigera felen i en vanlig dator är att starta med flera identiska bitar. I stället för att skriva 1 skrivs 111, och i stället för 0 skrivs 000. Så om någon bit på vägen blir fel, och dyker upp som 101 i stället för 111, så går det att rätta till. Men metoden går inte att tillämpa på kvantbitar, eftersom dessa inte kan kopieras eller avläsas utan att deras superpositionstillstånd förstörs.
Återigen var det Peter Shor som visade hur man skulle gå till väga. Han konstruerade en felkorrigeringsmetod. Med den kan tillförlitliga kvantberäkningar utföras även om det dyker upp fel på vägen. Men metoden kan bara rätta till ett fel åt gången, så det är viktigt att hinna korrigera varje fel innan nästa fel uppkommer. Annars skulle felen staplas på varandra.
Det går att uppskatta ett tröskelvärde för hur ofta kvantgrindar kan tillåtas utföra felaktiga operationer för att kvantberäkningarna, inklusive felkorrigeringar, fortfarande ska vara korrekta. En uppskattning är att gränsen ligger på ett fel per tiotusen till en miljon kvantgrindsoperationer. Dagens kvantdatorer är inte ens i närheten av detta värde.
Då gäller det att hitta en kvantgrind som inte gör fel lika ofta, så att man hinner korrigera felen. För ett par år sedan kom vi med ett förslag på en ny metod där operationerna kan göras mycket snabbare, så att inte lika många fel ska hinna uppstå. Metoden har nu testats i ett flertal lyckade experiment, bland annat med kvantbitar som består av supraledande kretsar och defekter i diamanter.
Fortfarande befinner sig den experimentella kvantdatorforskningen på ett stadium där endast ett fåtal kvantbitar kan kontrolleras. En lovande metod för att bygga en kvantdator är att använda så kallade jonfällor som David Wineland, Nobelpristagare 2012 i fysik, är expert på. Joner är elektriskt laddade atomer som kan fångas i en elektromagnetisk fälla. Olika energi hos var och en av jonerna representerar en kvantbit och kan manipuleras med laserljus. Hittills har man experimentellt lyckats kontrollera upp till 14 sådana kvantbitar, men i princip skulle de kunna bli godtyckligt många. Felkorrigeringar och mätningar på jonerna är inte heller något problem att utföra. Joner kan dessutom växelverka, prata med varandra, via kontrollerade vibrationer hos fällan, så det går utmärkt att bygga kvantgrindar som opererar på par av jon-kvantbitar.
Några andra lovande utföranden av kvantdatorns hårdvara bygger på supraledare eller defekter i diamanter. Stora tekniska utmaningar återstår dock att lösa innan vi kan säga att vi har en användbar kvantdator. Rekordet i dag ligger på 20 kvantbitar, och det är långt från de tusentals kvantgrindar som skulle krävas för att faktorisera ett 300 siffror långt tal.
Desto mer paradoxalt kan det kanadensiska D-waveföretaget verka, som nu hävdar att de har åstadkommit en dator med 512 kvantbitar. Det skulle innebära att D-wave bör kunna lagra 2512 tal i en kvantmekanisk superposition, en enorm mängd information som skulle kunna användas till fantastiska beräkningar. Än har vi inte sett dessa.
D-wavemaskinen är nämligen inte en kvantdator i en traditionell mening, även om kvanteffekter har viss betydelse för hur den fungerar. Den bygger på supraledande kvantbitar, där kvantfluktuationer, en sorts berg och dalar i energilandskapet, utnyttjas för att lösa olika typer av optimeringsproblem. I traditionella kvantdatorer är fluktuationer ett problem som måste korrigeras, men i D-wavemaskinerna är det just fluktuationerna som används för att utföra beräkningen. Det är främst tunneleffekten, en kvantmekanisk förmåga att ta sig igenom energibarriärer, som utnyttjas i D-wavedatorn. Men vi vet inte om tunneleffekten räcker för att få samma effektivitet som en kvantdator. Så det är fortfarande en öppen fråga om huruvida kvantfluktuationsdrivna datorberäkningar faktiskt är bättre än konventionella datorer.
Vad kvantdatorn ska användas till i framtiden vet vi inte, på samma sätt som det förr var omöjligt att förutspå alla tillämpningar av dagens datorer. Många problem väntar på effektivare lösningar, från resvägsplanering, bildigenkänning, gen- och proteinforskning, till riskanalyser och materialforskning.
Där den klassiska datorn kommer till korta hoppas vi att kvantdatorn kan komma till nytta.
Om forskarna

Erik Sjöqvist är professor i kvantinformationsteori vid Uppsala universitet. Hans modell för hur fel kan reduceras i kvantdatorberäkningar har nyligen testats vid flera laboratorier med lyckade resultat.
Marie Ericsson är docent vid Uppsala universitet och forskar om kvantinformation, med fokus på kvantinterferens och korrelationer för kvantsystem.









































