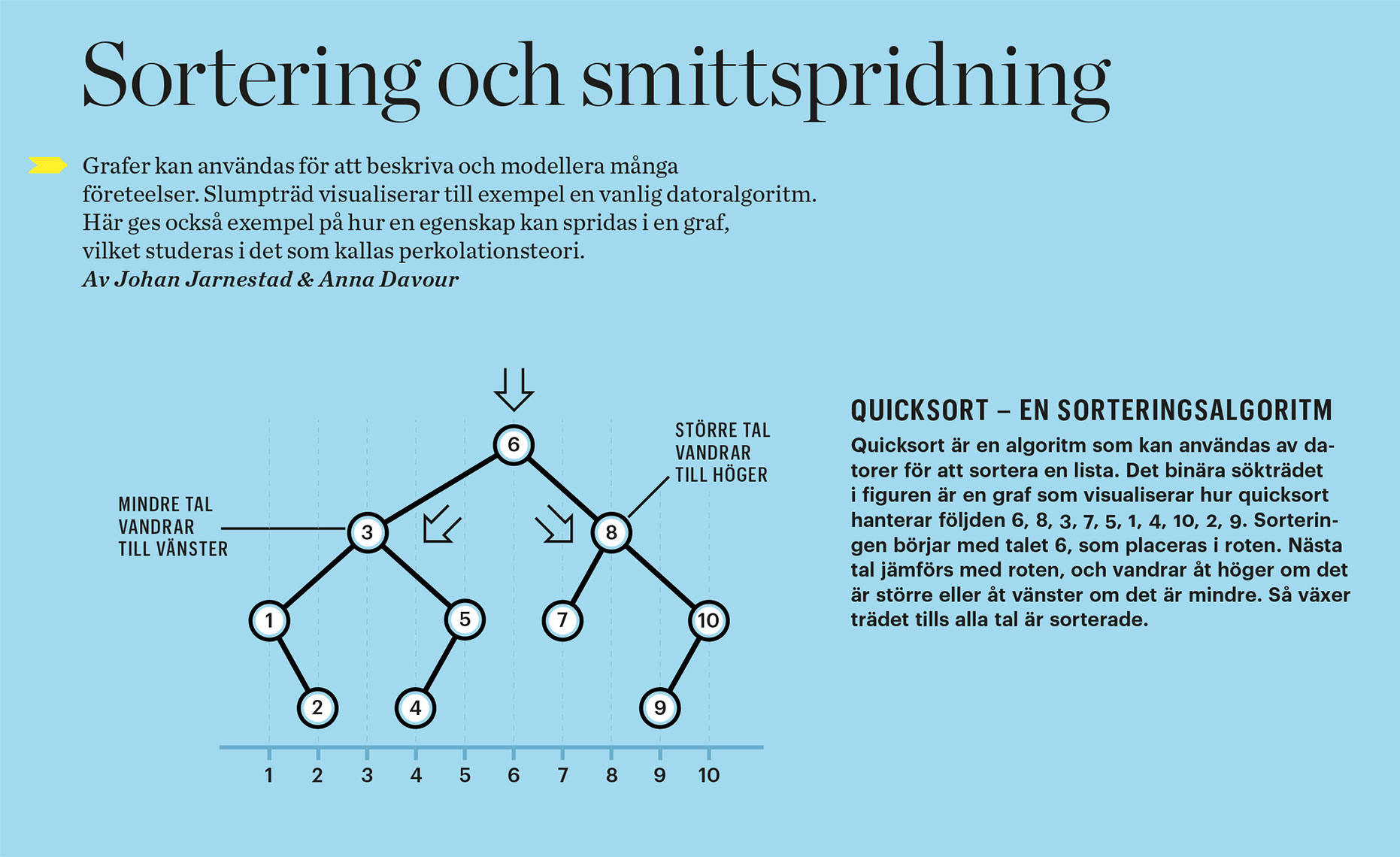
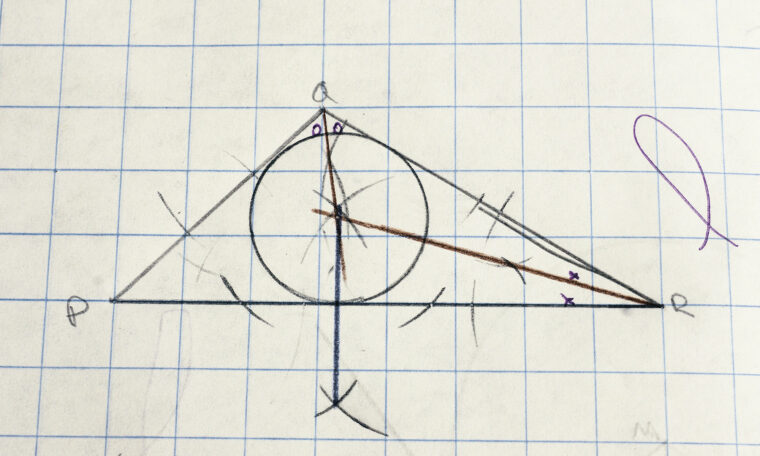
Matematikern Cecilia Holmgren ritar sina slumpträd direkt på väggen. Hon undersöker hur rykten fortplantas eller smittsamma sjukdomar sprids. ”Lösningar kommer ofta när man minst anar det”, säger hon.
Bild: Johan Marklund
Hennes matematik visar hur rykten och smittor sprids
Hur sprids rykten eller smittor? Det kan matematikern Cecilia Holmgren reda ut. I matematiska träd utforskar hon slump och sannolikhet.
Hur rykten fortplantar sig i sociala nätverk, hur en smittsam sjukdom sprids i befolkningen eller vad som avgör om släktnamn dör ut eller lever kvar. Det är några exempel på frågor som kan utforskas inom en gren av matematiken som kallas grafteori. Företag som Google och Amazon anställer matematiker som använder grafteori för att utveckla de algoritmer som används för sökningar och rekommendationer på nätet. Microsoft är ett annat företag som har anställt ledande grafteoriexperter, för att arbeta både med grundforskning och med tillämpningar. Fältet är också hett inom AI-forskningen.
Löser matematiska problem i grupp
För att få veta mer om detta område beger jag mig till Matematiska institutionen på Uppsala universitet för att möta en forskare inom grafteori.
De ljusa korridorerna på institutionen är folktomma vid den här tiden på förmiddagen, men Cecilia Holmgren visar den plats där hennes forskargrupp brukar hålla sina möten. Matematikforskning handlar numera mycket om att samarbeta och tänka tillsammans.
– För inte alltför längesedan sågs matematik som ett typiskt ensamjobb, men på senare år har det blivit vanligare att lösa problem i grupp. Jag tycker själv att det är allra roligast att lösa problem tillsammans med andra, säger Cecilia Holmgren.
Vrån ser nästan ut som en lekhörna, med designade sittmöbler och gott om utrymme för att skriva och rita på väggarna.
Cecilia Holmgren har fyllt en tavla med ett stort diagram, som sitter ihop upptill men förgrenar sig nedåt som ett stort rotsystem – men i matematiken kallas detta för ett träd. Trädet är en typ av graf. Grafteori är ett matematiskt fält som ger många tillfällen att rita figurer.
– Mina föredrag brukar bygga på bilder, berättar hon.
Två sorters graf inom matematiken
Förvirrande nog finns det två helt olika betydelser av ordet ”graf” inom matematiken. Den första sortens graf, som vi stöter på i skolan, är en sorts diagram som visar ett samband mellan olika variabler. Men i grafteorin är graf en struktur med punkter – noder – som är sammankopplade med streck som kallas kanter.
Olika typer av grafer har olika matematiska egenskaper, beroende på till exempel om alla noder är ihopkopplade och hur många kanter som går till varje nod.
Grafteori har många tillämpningar, eftersom graferna kan användas som modell för situationer i verkligheten. Noderna kan till exempel stå för webbplatser och kanterna representera länkar mellan dem. Eller så kan noderna vara personer, och kanterna får stå för någon typ av kontakt mellan dem – sexuella relationer eller handskakningar mellan bekanta, eller vilka som följer varandra i sociala medier.
Du kanske har hört att det bara är sex led mellan dig och vem som helst i världen. Du känner någon som känner någon, och så vidare, och i sex steg kan du nå fram till vilken nu levande person som helst. Det är ett resultat från grafteori, berättar Cecilia Holmgren.
– Om varje person bara känner drygt en person i snitt räcker det för att majoriteten av befolkningen hänger ihop i en stor graf. I verkligheten är det vanligt att ha ungefär 1 000 bekanta.
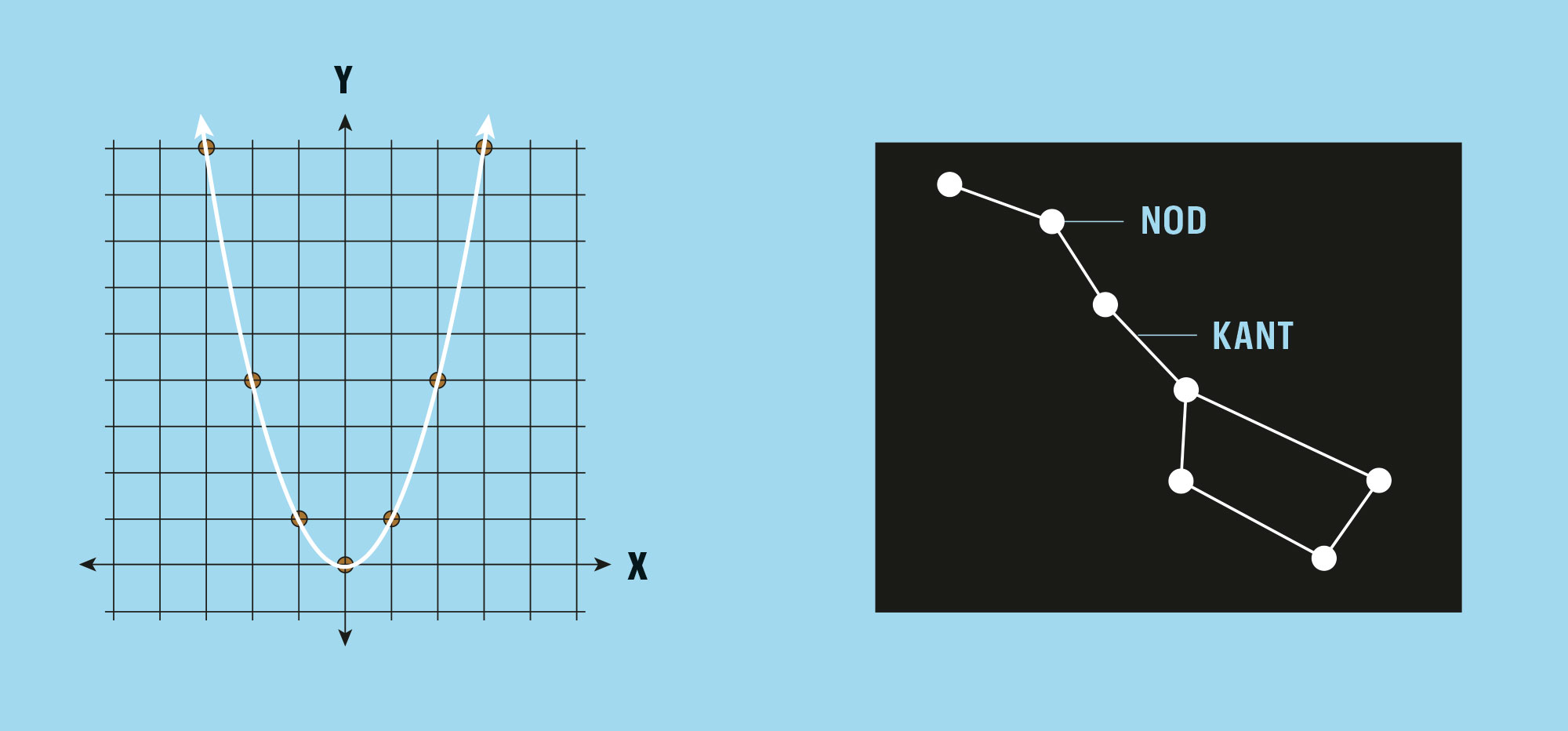
Bild: Johan Jarnestad
Matematiker har undersökt hur långt det är mellan olika noder i en graf som efterliknar människors verkliga kontakter. Det visar sig att det blir extremt låg sannolikhet för att det blir mer än sex steg mellan vilka slumpmässigt valda noder som helst.
– För de flesta personer är det bara tre eller fyra steg emellan, säger Cecilia Holmgren.
Det här är ett ganska begripligt exempel, som illustrerar vad forskare i grafteori får fram för typ av resultat – de hittar formler eller sannolikhetsfördelningar som beskriver egenskaperna hos olika typer av grafer. När matematikerna undersöker hur många led det är mellan två slumpmässiga personer på jorden, beräknar de hur längden mellan två noder varierar beroende på hur tätt hopkopplad grafen är – alltså hur många kontakter varje person har i genomsnitt.
Här finns bara en väg mellan två noder
När jag tittar igenom titlar och sammanfattningar på Cecilia Holmgrens vetenskapliga publikationer från de senaste åren, är de fulla av termer och uttryck som är ogenomskinliga för mig. (En av titlarna är The asymptotic non-normality of the giant cluster for percolation on random split trees.) Jag kan förstå så mycket som att det handlar om hur olika egenskaper hos graferna hänger ihop med varandra, och hur de ändras när graferna påverkas på olika sätt. Men vissa saker klarnar när Cecilia Holmgren själv berättar om dem.
Hennes arbete handlar mycket om den speciella typen av grafer som kallas träd, som det hon har ritat upp på tavlan. En speciell sak med den här typen av graf är att det bara finns en väg mellan två noder.
Slumpträd är en form av slumpgrafer. Slumpgrafer konstrueras genom att dela ut egenskaperna i grafen på ett slumpmässigt sätt: antalet noder, antalet kanter, och hur kanterna kopplar ihop noderna. Slumpträd börjar med en nod i roten, och sedan läggs grenarna till med någon slumpfaktor. Cecilia Holmgren har arbetat mycket med en klass av slumpträd som kallas splitträd. Det enklaste exemplet är något som kallas binära sökträd, som har en direkt koppling till datavetenskapen. Avståndet mellan roten och de yttersta noderna, ”löven”, på ett sökträd ger ett mått på hur effektiv den motsvarande sökalgoritmen är.
Cecilia Holmgren har bland annat jobbat med att hitta allmänna beskrivningar av hur avstånden mellan olika noder inuti alla möjliga olika typer av sådana träd utvecklas, beroende på olika parametrar.
– I min forskning är jag intresserad av att visa generella resultat som gäller för alla träd på en gång. Tidigare forskning har som regel bara studerat en typ av träd i taget, säger hon.
Undersöker hur smitta sprids
Hon jobbar också med problem som påminner om hur rykten eller smittor sprids. Man kan markera slumpmässiga noder i en graf som ”smittade”, och sedan får smittan spridas längs kanterna till andra noder enligt någon given regel. En sådan regel kan vara att om en nod har minst två smittade grannar så blir den också smittad. Sedan undersöker man hur smittan sprids genom grafen, och hur stor del av grafen som nås.
Studiet av grafers egenskaper när man förändrar dem enligt vissa regler, som när smittan sprids, kallas på matematikspråk för perkolation. Ordet kanske känns igen från kaffebryggning, och teorin för perkolation har mycket riktigt sitt ursprung i modeller för hur vätskor kan flöda fram genom porösa material – precis som när vattnet sipprar genom de malda kaffebönorna.
Perkolationsteorin använder hon för att studera speciella fall där en liten förändring gör att slutresultatet blir helt annorlunda.
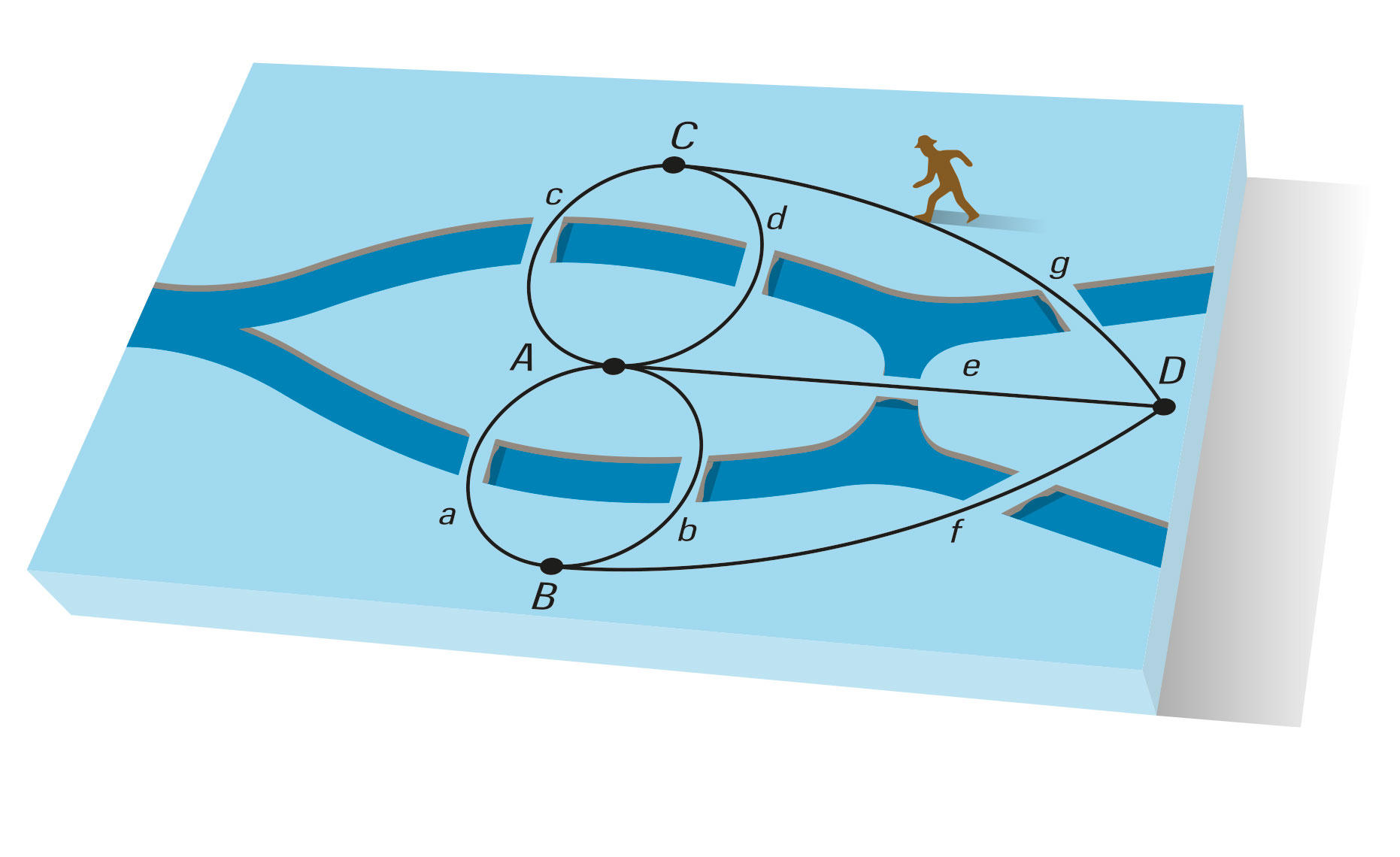
Bild: Johan Jarnestad
Ett exempel är sannolikheten för att ett släktnamn ska överleva eller dö ut. Det studerades först av forskarna Francis Galton och Henry William Watson på 1800-talet, som var intresserade av brittiska adelssläkter. Släkten börjar med en man, och varje familjemedlem får ett slumpmässigt antal söner som kan föra släktnamnet i arv. Det finns en sannolikhet för att släktnamnet ska överleva för evigt om medelvärdet av antalet söner per person är större än 1. Om medelvärdet är mindre än 1 dör släktnamnet alltid ut. När medelvärdet är större än 1 kan namnet leva för evigt, vilket betyder att trädet blir oändligt högt. Medelvärdet 1 av antal söner per person är alltså en brytpunkt mellan ändliga och oändliga träd.
Sådana brytpunkter för förändringar kallas för fasövergångar, i analogi med fysiken där en mycket liten ändring i tryck eller temperatur kan få ett ämne att helt ändra karaktär genom att det smälter, stelnar eller förångas.
Vänskapsparadoxen ett klassiskt problem
På liknande sätt finns det också fasövergångar i spridningar av en ”smitta” i grafen. Cecilia Holmgren studerar vilka sannolikheter som behövs för att smitta en hel graf, givet olika förutsättningar. Från början låter man varje nod vara smittad med en viss sannolikhet och sedan låter man smittan spridas enligt den givna regeln. Om sannolikheten för att en nod är smittad från början är lite över ett kritiskt värde, kommer hela grafen att smittas, annars inte.
Medan vi pratar om smittor berättar Cecilia Holmgren om ett annat klassiskt problem i grafteori, som kallas för vänskapsparadoxen. Om du bara har få vaccindoser men vill skydda befolkningen så bra som möjligt – vad är bästa sättet för att fördela vaccinet?
– Det visar sig att det bästa är att fördela vaccinet slumpmässigt, men att be varje person som får vaccinet att i stället för att ta det själv ge det till en kompis. Den som får vaccin är då troligtvis en social person, som utan vaccin skulle ha spritt sjukdomen effektivt.
Skärning mellan sannolikhetsteori och kombinatorik
Att hennes forskning kom in på slumpgrafer var delvis en tillfällighet. Hon sökte sig till Uppsala för att få göra sin doktorsavhandling med professor Svante Janson som handledare, en av de världsledande forskarna inom ämnet slumpgrafer. Cecilia Holmgren tycker att det är en rolig och intressant del av matematiken.
– Jag gillar att det är en skärning mellan sannolikhetsteori och kombinatorik. Kombinatoriken innehåller kluriga lösningar, och sannolikhetsteorin har en djup teoretisk grund.
För en utomstående kan det vara svårt att förstå hur en matematiker arbetar. Det är inte som att gå till ett laboratorium och ställa upp ett experiment. Cecilia Holmgren berättar att hon ofta har en idé om vilka metoder hon vill försöka använda, när hon står inför ett givet problem. En del av det kommer med erfarenhet, genom att hon har lärt sig allt fler olika matematiska metoder och även att kombinera dem.
– Ändå kommer lösningar ofta när man minst anar det. Ofta går jag och tänker på mina matematiska problem även när jag inte är medveten om det, och det har hänt flera gånger att jag löst viktiga problem medan jag till exempel har ridit min häst.

Kunskap baserad på vetenskap
Prenumerera på Forskning & Framsteg!
Inlogg på fof.se • Tidning • Arkiv med tidigare nummer