Raka vägen över dodekaedern
Dodekaedern har tolv sidor, som vardera har fem kanter. Den här formen är känd och utforskad sedan Euklides tid för 2300 år sedan, men nu har matematiker gjort en ny upptäckt om vilka raka vägar som går att ta över dodekaederns yta.
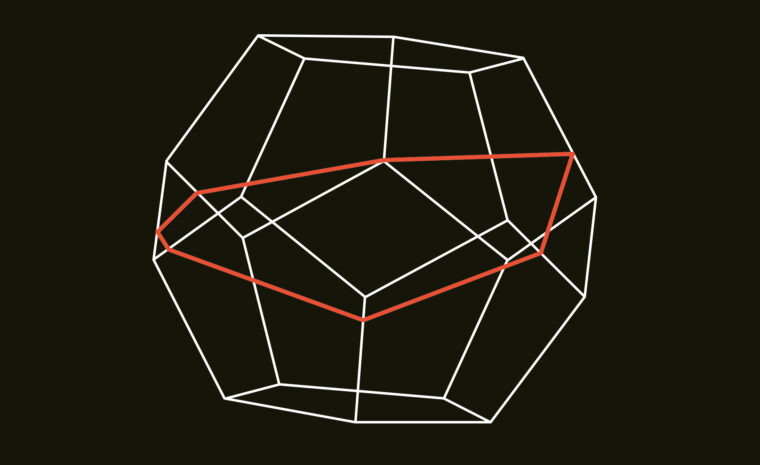
Bild: W. Patrick Hooper, Jayadev S. Athreya och David Aulicino
Det finns inget sätt att utgå från ett hörn på en kub och dra en rak linje över kubens yta som kommer tillbaka till samma punkt, utan att gå genom ett annat hörn. Men hur är det egentligen med andra regelbundna tredimensionella figurer?
Sedan antiken har matematiker känt till fem tredimensionella figurer som har platta sidor, där alla kanter är lika långa. De brukar kallas för de platonska kropparna. Kuben, som har sex kvadratiska sidor, är den mest välbekanta. Sedan finns det fyra till: tetraedern, oktaedern och ikosaedern som har fyra, åtta, respektive tjugo liksidiga trianglar som sidor, och dodekaedern som består av tolv pentagoner.
Redan tidigare visste matematiker att det inte går att ta en rak väg från ett hörn och tillbaka över de övriga platonska kropparna, men de har inte vetat hur det ligger till med dodekaedern. Nu har tre amerikanska matematiker utforskat denna fråga.
Först hittade de ett bevis för att en sådan väg faktiskt finns. Beviset är i form av en figur, med vägen utritad.
Sedan gick de vidare med att utforska vilka typer av sådana vägar som går att ta. Det visar sig finnas 31 olika klasser av raka vägar från ett hörn tillbaka till samma hörn, beroende på i vilken riktning man startar. De skiljer sig åt i hur många gånger de korsar sig själva innan de återvänder till startpunkten. Nu vet de alltså inte bara att det finns en lösning, utan de har kartlagt alla de olika formerna en sådan lösning kan ta.
Även till synes välkända och välutforskade matematiska fenomen kan efter några tusen år bjuda på nya insikter.